यूनिवर्स के रहस्यों को सुलझाना: मर्सेन ट्विस्टर, नंबर्स और टेक्नोलॉजी पर उनके असर के लिए एक पूरी गाइड

मेर्सेन ट्विस्टर (Mersenne Twister) एक बहुत लोकप्रिय और कुशल छद्म यादृच्छिक संख्या जनरेटर (PRNG) एल्गोरिदम है, जिसका उपयोग कंप्यूटरों में उन अनुक्रमों को बनाने के लिए किया जाता है जो यादृच्छिकता की नकल करते हैं, उदाहरण के लिए, गेम्स, सिमुलेशन और सांख्यिकी में। यह अपने विशाल अवधि (अनुक्रम केवल बहुत बड़ी संख्या में संख्याओं के बाद दोहराता है, ~4.3×10^6001), उत्पादन की उच्च गति और अच्छी सांख्यिकीय गुणवत्ता के लिए जाना जाता है, लेकिन क्रिप्टोग्राफी के लिए उपयुक्त नहीं है, क्योंकि इसकी स्थिति को पुनर्प्राप्त किया जा सकता है यदि 624 उत्पन्न संख्याएँ ज्ञात हों।

मेर्सेन ट्विस्टर एक भौतिक घटना नहीं है, बल्कि एक रूपक नाम है जिसका उपयोग गणित और कंप्यूटर विज्ञान में मेर्सेन अभाज्य संख्याओं के गुणों पर आधारित छद्म यादृच्छिक संख्या उत्पादन के एक कुशल एल्गोरिदम का वर्णन करने के लिए किया जाता है। यह एल्गोरिदम, जिसे मेर्सेन ट्विस्टर या Mersenne Twister के रूप में जाना जाता है, अपनी असाधारण रूप से लंबी आवर्तकाल, मेर्सेन संख्या M_19937 के बराबर, जिसका अर्थ है 2^19937 – 1, और यादृच्छिक संख्याओं के वितरण की उच्च गुणवत्ता के लिए विशेष रूप से मूल्यवान है।

मेर्सेन ट्विस्टर का व्यावहारिक मूल्य मॉडलिंग, क्रिप्टोग्राफी (चेतावनियों के साथ), कंप्यूटर गेम्स और वैज्ञानिक कंप्यूटिंग के लिए इसके व्यापक उपयोग में निहित है, जहां एक विश्वसनीय यादृच्छिकता स्रोत की आवश्यकता होती है। इस एल्गोरिदम की समझ मेर्सेन संख्याओं के अध्ययन से अविभाज्य रूप से जुड़ी हुई है – M_n = 2^n – 1 के रूप की संख्याएँ, जो केवल कुछ शर्तों के तहत अभाज्य होती हैं और जिन्होंने सदियों से गणितज्ञों के दिमाग को उत्तेजित किया है।

यह मेर्सेन अभाज्य संख्याओं, सबसे बड़ी ज्ञात अभाज्य संख्याओं की खोज, और कंप्यूटिंग सिस्टम के लिए उच्च-गुणवत्ता वाले यादृच्छिक संख्या जनरेटर की आवश्यकता थी जिसके कारण इस उत्कृष्ट एल्गोरिदम का निर्माण हुआ, जो कई प्रोग्रामिंग भाषाओं और सिस्टमों में एक मानक बन गया है।

मेर्सेन ट्विस्टर क्या है और यह इतना महत्वपूर्ण क्यों है?

जब लोग मेर्सेन ट्विस्टर के बारे में बात करते हैं, तो उनका आमतौर पर मतलब एक विशिष्ट एल्गोरिदम – Mersenne Twister (MT19937) से होता है, जिसे 1997 में जापानी वैज्ञानिक माकोतो मात्सुमोतो और ताकुजी निशिमुरा द्वारा विकसित किया गया था। इस एल्गोरिदम का मुख्य कार्य संख्याओं का एक अनुक्रम उत्पन्न करना है जो यादृच्छिक के जितना संभव हो उतना करीब है, लेकिन साथ ही पूरी तरह से नियतात्मक और पुनरुत्पादनीय है जब एक ही प्रारंभिक मान (seed) दिया जाता है।

यह गुण वैज्ञानिक प्रयोगों के लिए महत्वपूर्ण है जहां सिमुलेशन के परिणाम सत्यापन योग्य होने चाहिए। साधारण रैखिक संगत जनरेटरों के विपरीत, जिनकी अवधि छोटी होती है और जो पूर्वानुमेय परिणाम दे सकते हैं, मेर्सेन ट्विस्टर 623 आयामों तक संख्याओं का एक समान वितरण प्रदान करता है, जिससे यह सामान्य उपयोग के लिए सबसे विश्वसनीय जनरेटरों में से एक बन जाता है।

इसका विकास 90 के दशक के मध्य में कम्प्यूटेशनल गणित की बढ़ती आवश्यकताओं की प्रतिक्रिया थी, जब मौजूदा एल्गोरिदम जटिल प्रणालियों के मॉडलिंग के कार्यों को संभालने में असमर्थ हो गए थे।

Mersenne Twister एल्गोरिदम के मुख्य गुण क्या हैं?

मेर्सेन ट्विस्टर एल्गोरिदम में विशेषताओं का एक समूह है जो इसे एक उत्कृष्ट उपकरण बनाता है। सबसे पहले, इसकी अवधि अविश्वसनीय रूप से लंबी है और 2^19937 – 1 है, जो ब्रह्मांड में प्राथमिक कणों की संख्या से अधिक है। यह संख्या एक मेर्सेन अभाज्य संख्या है, इसलिए एल्गोरिदम का नाम। दूसरा, यह अपने संपूर्ण अवस्था स्थान में मूल्यों का एक समान वितरण प्रदान करता है, जिसकी पुष्टि कठोर सांख्यिकीय परीक्षणों जैसे कि Diehard tests द्वारा की जाती है। तीसरा, यह बिटवाइज़ ऑपरेशन का उपयोग करके आधुनिक कंप्यूटर हार्डवेयर पर कुशलता से कार्यान्वित किया जाता है और इसमें अच्छा प्रदर्शन होता है। हालांकि, यह ध्यान रखना महत्वपूर्ण है कि एल्गोरिदम क्रिप्टोग्राफिक रूप से सुरक्षित नहीं है: क्रमागत आउटपुट मूल्यों की पर्याप्त संख्या जानने पर, कोई आंतरिक स्थिति को पुनर्प्राप्त कर सकता है और संपूर्ण बाद के अनुक्रम की भविष्यवाणी कर सकता है। इसलिए, सुरक्षा से संबंधित कार्यों के लिए, अन्य विशिष्ट जनरेटरों का उपयोग किया जाता है।

वास्तविक अनुप्रयोगों में मेर्सेन ट्विस्टर का उपयोग कैसे किया जाता है?

इसके गुणों के कारण, Mersenne Twister कई लोकप्रिय सिस्टम में मानक यादृच्छिक संख्या जनरेटर बन गया है। उदाहरण के लिए, यह प्रोग्रामिंग भाषाओं जैसे Python (रैंडम मॉड्यूल), R, Ruby, PHP और सामान्य गणितीय पैकेज जैसे MATLAB में डिफ़ॉल्ट जनरेटर है। कंप्यूटर गेम्स में, इसका उपयोग अक्सर स्तरों, घटनाओं और गैर-खिलाड़ी चरित्र व्यवहार को उत्पन्न करने के लिए किया जाता है, जिससे एक विविध और फिर भी पुनरुत्पादनीय गेमिंग अनुभव बनता है। वैज्ञानिक अनुसंधान में, विशेष रूप से भौतिकी, वित्तीय मॉडलिंग और बायोइनफॉरमैटिक्स के लिए मोंटे कार्लो विधियों में, यह एल्गोरिदम सांख्यिकीय रूप से महत्वपूर्ण परिणाम प्राप्त करने के लिए आवश्यक यादृच्छिकता प्रदान करता है।

मशीन लर्निंग परियोजनाओं पर काम करने के व्यक्तिगत अनुभव से, मैं कह सकता हूं कि तंत्रिका नेटवर्क के वज़नों का आरंभीकरण अक्सर एक गुणवत्तापूर्ण यादृच्छिक संख्या जनरेटर पर निर्भर करता है, और मेर्सेन ट्विस्टर लंबे समय तक इस कार्य के लिए एक विश्वसनीय विकल्प था, जब तक कि अधिक विशिष्ट विधियाँ सामने नहीं आईं।

ट्रेडिंग और निवेश में मेर्सेन ट्विस्टर को सही ढंग से कैसे आरंभ और उपयोग करें?

वित्तीय मॉडलिंग, एल्गोरिदमिक ट्रेडिंग और निवेश जोखिम मूल्यांकन में मेर्सेन ट्विस्टर का आरंभ और उपयोग नियतात्मकता और यादृच्छिकता की गुणवत्ता पर विशेष ध्यान देने की मांग करता है।

मुख्य सिद्धांत व्यापार रणनीतियों के बैकटेस्टिंग परिणामों की गारंटीकृत पुनरुत्पादन क्षमता है। इसे प्राप्त करने के लिए, जनरेटर का प्रारंभिक मान (seed) कोड में एक स्थिरांक के रूप में स्पष्ट रूप से निर्धारित किया जाना चाहिए, न कि सिस्टम के वर्तमान समय पर निर्भर। यह “यादृच्छिक” घटनाओं के पूरे अनुक्रम – मूल्य झटके, ऑर्डर निष्पादन समय – को सटीक रूप से पुनः बनाने की अनुमति देता है और यह सुनिश्चित करता है कि रणनीति की लाभप्रदता कई टेस्ट रन में स्थिर है, न कि एकल भाग्यशाली सिमुलेशन का परिणाम।

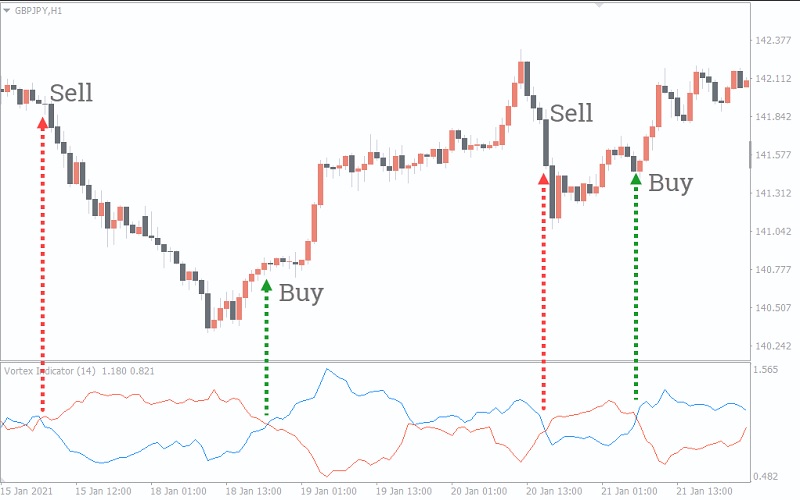
उच्च-लोड ट्रेडिंग सिस्टम में जो कई डेटा स्ट्रीम प्रोसेस करते हैं, प्रत्येक तार्किक मॉड्यूल (जैसे, बाजार प्रभाव सिम्युलेटर, अनुकूलन के लिए पैरामीटर जनरेटर, और जोखिम मूल्यांकन मॉड्यूल) को एक अद्वितीय, लेकिन यह भी नियतात्मक seed के साथ अपने स्वयं के, पृथक जनरेटर उदाहरण का उपयोग करना चाहिए। यह यादृच्छिक प्रक्रियाओं के बीच अंतर्निहित सहसंबंध को रोकता है, जो अंतिम आँकड़ों जैसे अधिकतम ड्राडाउन या शार्प अनुपात को विकृत कर सकता है।

संपत्ति मूल्य पथों के मॉडलिंग के लिए, उदाहरण के लिए, विकल्प मूल्य निर्धारण या वैल्यू एट रिस्क (VaR) के लिए मोंटे कार्लो पद्धति का उपयोग करते हुए, एक समान वितरण `random()` का मानक कॉल अक्सर अपर्याप्त होता है। मेर्सेन ट्विस्टर से समान रूप से वितरित अनुक्रम को अन्य सांख्यिकीय वितरणों, जैसे सामान्य या लॉगनॉर्मल में बदलना आवश्यक है, जिसके लिए बॉक्स-मुलर परिवर्तन जैसे एल्गोरिदम का उपयोग किया जाता है। साथ ही, वित्तीय क्षेत्र के लिए एल्गोरिदम की मुख्य कमी – पर्याप्त लंबे आउटपुट अनुक्रम का अवलोकन करने पर इसकी पूर्वानुमेयता – को समझना और उसकी क्षतिपूर्ति करना अत्यंत महत्वपूर्ण है।

हालांकि शुद्ध रूप से शोध उद्देश्यों के लिए बैकटेस्टिंग में यह कोई समस्या नहीं है, लेकिन लाइव ट्रेडिंग सिस्टम के कामकाज के लिए, जहां यादृच्छिकता का उपयोग ऑर्डर सबमिशन समय को यादृच्छिक बनाने के लिए किया जा सकता है, यह कारक एक सैद्धांतिक कमजोरी का प्रतिनिधित्व करता है। इसलिए, उत्पादन वातावरण में, विशेष रूप से उच्च-आवृत्ति ट्रेडिंग में, अक्सर संकर दृष्टिकोणों का उपयोग किया जाता है, जहां मेर्सेन ट्विस्टर, जिसे एक सुरक्षित क्रिप्टोग्राफिक seed के साथ आरंभ किया गया है, को आवधिक स्थिति अद्यतन के लिए हार्डवेयर यादृच्छिक संख्या जनरेटरों से वास्तविक एन्ट्रॉपी के स्रोत के साथ जोड़ा जाता है।

जोखिम प्रबंधन अनुभव से एक व्यावहारिक उदाहरण: ऐतिहासिक मोंटे कार्लो सिमुलेशन का उपयोग करके पोर्टफोलियो के लिए VaR की गणना करते समय, हमने भविष्य की कीमतों के सैकड़ों हजारों परिदृश्य उत्पन्न किए। मॉडल विकास चरण के दौरान एक निश्चित seed के साथ मेर्सेन ट्विस्टर का उपयोग करने से विश्लेषकों की पूरी टीम को समान डेटा के साथ काम करने और नए कारकों के प्रभाव की लगातार जांच करने की अनुमति मिली। हालाँकि, नियामक के लिए अंतिम रिपोर्ट में, seed बदल दिया गया था, और VaR मीट्रिक के लिए आत्मविश्वास अंतराल प्राप्त करने के लिए संपूर्ण गणना को एक हज़ार बार दोहराया गया, जिसने मॉडल की मजबूती प्रदर्शित की।

यह दो-चरणीय दृष्टिकोण – विकास और सत्यापन के लिए नियतात्मकता प्लस अंतिम मूल्यांकन के लिए परिवर्तनशीलता – एक अच्छा अभ्यास है। यह एक विशिष्ट यादृच्छिक अनुक्रम के लिए एक व्यापार रणनीति के “ओवरफिटिंग” से बचने में भी मदद करता है: यदि एक रणनीति केवल एक पूर्वनिर्धारित seed पर लाभ दिखाती है लेकिन दूसरे सौ पर “असफल” हो जाती है, तो यह सांख्यिकीय महत्वहीनता और शोर के अनुकूल वक्र समायोजन का एक स्पष्ट संकेत है।

इस प्रकार, मेर्सेन ट्विस्टर वित्त में एक नियंत्रित स्टोकेस्टिक वातावरण बनाने के लिए एक विश्वसनीय और कुशल उपकरण के रूप में कार्य करता है। इसका उचित अनुप्रयोग तीन स्तंभों पर बनाया गया है: परीक्षणों की पुनरुत्पादन क्षमता के लिए सख्त नियतात्मकता, प्रयोगों की शुद्धता के लिए जनरेटर अलगाव, और अंतिम विश्लेषण के चरण में और परिचालन प्रणालियों में परिवर्तनशीलता और क्रिप्टोग्राफिक रूप से सुरक्षित यादृच्छिकता स्रोतों के लिए सचेत संक्रमण। यह एल्गोरिदम बाजार की अनिश्चितता को मात्रात्मक रूप से मापने योग्य जोखिमों और अवसरों में बदलने की अनुमति देता है, निवेश निर्णय लेने में गणितीय कठोरता सुनिश्चित करता है।

मेर्सेन संख्याओं की आवश्यकता क्यों है और उन्हें क्या विशेष बनाता है?

मेर्सेन संख्याएँ, 17वीं सदी के फ्रांसीसी साधु मारिन मेर्सेन के नाम पर, M_n = 2^n – 1 के रूप की हैं। उनका अध्ययन अमूर्त जिज्ञासा से नहीं, बल्कि संख्या सिद्धांत और व्यावहारिक अनुप्रयोगों के साथ मौलिक संबंधों के कारण किया जाता है।

मेर्सेन अभाज्य संख्याएँ पूर्ण संख्याओं से सीधे जुड़ी हुई हैं – वे संख्याएँ जो अपने स्वयं के उचित भाजकों के योग के बराबर होती हैं। यूक्लिड द्वारा सिद्ध और बाद में ऑयलर द्वारा पूरक एक प्रमेय के अनुसार, प्रत्येक सम पूर्ण संख्या को 2^(p-1) * (2^p – 1) के रूप में दर्शाया जा सकता है, जहाँ (2^p – 1) एक मेर्सेन अभाज्य संख्या है।

यह गहरा संबंध उन्हें पूर्ण संख्याओं की संरचना को समझने की कुंजी बनाता है। इसके अलावा, मेर्सेन अभाज्य संख्याएँ नई अभाज्यता परीक्षण एल्गोरिदम और शक्तिशाली कंप्यूटिंग प्रणालियों के लिए परीक्षण मैदान के रूप में कार्य करती हैं, जैसे कि GIMPS परियोजना (ग्रेट इंटरनेट मेर्सेन प्राइम सर्च) में। अपने द्विआधारी प्रकृति (द्विआधारी प्रणाली में लगातार इकाइयों का क्रम) के कारण उनका कंप्यूटर विज्ञान में भी महत्व है, उदाहरण के लिए, त्रुटि-सुधार कोड के निर्माण में।

मेर्सेन अभाज्य संख्याओं की खोज के पीछे का इतिहास क्या है?

मेर्सेन अभाज्य संख्याओं का शिकार एक सदियों पुरानी गाथा है जो त्रुटियों, विजयों और तकनीकी प्रगति से भरी हुई है। मेर्सेन ने स्वयं 1644 में दावा किया था कि 257 तक के n के कौन से मान अभाज्य संख्याएँ देते हैं, और उनके कई अनुमान गलत साबित हुए। गणितीय उपकरणों के विकास और कंप्यूटरों के आगमन के साथ ही खोज में तेजी आई।

एक मील का पत्थर घटना 1996 में GIMPS परियोजना की शक्ति द्वारा संख्या M_1398269 की खोज थी, जो दुनिया भर के हजारों स्वयंसेवकों से वितरित कंप्यूटिंग का उपयोग करती है। सबसे बड़ी ज्ञात अभाज्य संख्या की लगभग हर नई खोज एक मेर्सेन संख्या होती है, जो विशेषज्ञता प्राप्त जाँच एल्गोरिदम की दक्षता को दर्शाती है, जैसे कि लुकास-लेहमर परीक्षण। यह परीक्षण, 1930 के दशक में विकसित, मेर्सेन संख्या की अभाज्यता को अपेक्षाकृत तेजी से (संख्या सिद्धांत के मानकों द्वारा) जाँचने की अनुमति देता है, बिना सभी संभावित भाजकों द्वारा थकाऊ विभाजन किए। 1952 के बाद से, सभी रिकॉर्ड तोड़ने वाली अभाज्य संख्याएँ मेर्सेन संख्याओं के बीच पाई गई हैं।

मेर्सेन संख्याओं के आज व्यावहारिक अनुप्रयोग क्या हैं?

• क्रिप्टोग्राफी: हालांकि मेर्सेन संख्याएँ स्वयं आधुनिक क्रिप्टोग्राफिक प्रणालियों (जैसे RSA) का आधार नहीं हैं, लेकिन लुकास-लेहमर परीक्षण की दक्षता के कारण कुछ प्रोटोकॉल में आवश्यक बड़ी अभाज्य संख्याएँ उत्पन्न करने के लिए उनका उपयोग किया जाता है।
• कंप्यूटर हार्डवेयर परीक्षण: विशाल मेर्सेन संख्याओं के साथ संचालन प्रोसेसर और मेमोरी सिस्टम के लिए एक तनाव परीक्षण के रूप में कार्य करते हैं, फ़्लोटिंग-पॉइंट और पूर्णांक अंकगणित में त्रुटियों को उजागर करते हैं।
• कोडिंग सिद्धांत: उनकी द्विआधारी संरचना (उदाहरण के लिए M_3 = 7, जो द्विआधारी में 111 है) का चक्रीय कोड और डेटा संचरण में त्रुटियों को सही करने वाली अन्य योजनाओं के निर्माण में अनुप्रयोग होता है।
• गणितीय अनुसंधान: वे ऐसी अनसुलझी समस्याओं में केंद्रीय वस्तुएं बनी हुई हैं, जैसे कि मेर्सेन अभाज्य संख्याओं की अनंतता की परिकल्पना, जिसका समाधान संपूर्ण संख्या सिद्धांत को आगे बढ़ाएगा।

सबसे महत्वपूर्ण मेर्सेन संख्या: कौन सी है और क्यों?

कई उम्मीदवार मेर्सेन संख्या के सबसे महत्वपूर्ण होने के शीर्षक के लिए प्रतिस्पर्धा करते हैं, मानदंडों – ऐतिहासिक महत्व, गणितीय सुंदरता, या कम्प्यूटेशनल विजय के आधार पर। औपचारिक रूप से, आज तक का सबसे महत्वपूर्ण सबसे बड़ी ज्ञात अभाज्य संख्या है, जो 2026 तक एक मेर्सेन अभाज्य संख्या भी है। GIMPS परियोर्जना के भीतर स्थापित नवीनतम रिकॉर्ड संख्या M_82589933 है, जिसमें लगभग 25 मिलियन दशमलव अंक हैं।

हालाँकि, ऐतिहासिक और वैचारिक दृष्टिकोण से, संख्या M_31 = 2^31 – 1 = 2147483647 ने एक बहुत बड़ी भूमिका निभाई। यह संख्या एक मेर्सेन अभाज्य संख्या है और लंबे समय तक सबसे बड़ी ज्ञात अभाज्य संख्या थी, जिसे 1772 में लियोनहार्ड ऑयलर द्वारा खोजा गया था। लेकिन इससे भी महत्वपूर्ण बात यह है कि M_31 कंप्यूटर विज्ञान में 32-बिट साइन इंटीजर के लिए अधिकतम मूल्य है, जिसने इसे प्रोग्रामिंग में एक मौलिक स्थिरांक बना दिया, जो सरणियों, पहचानकर्ताओं और यादृच्छिक संख्याओं की सीमा निर्धारित करता है। कई प्रारंभिक यादृच्छिक संख्या जनरेटर, जिनमें मेर्सेन ट्विस्टर भी शामिल है, को प्रोसेसर आर्किटेक्चर की इस सीमा को ध्यान में रखकर विकसित किया गया था।

M_31 ने कंप्यूटर विज्ञान के विकास को कैसे प्रभावित किया?

संख्या 2^31 – 1 सॉफ्टवेयर डिजाइन की नींव में व्याप्त है। यह सी और सी ++ भाषाओं में डेटा प्रकार `int32_t` के लिए अधिकतम सकारात्मक सीमा निर्धारित करती है, जो डेटा संरचनाओं के डिजाइन, सरणी अनुक्रमण और अद्वितीय पहचानकर्ताओं के निर्माण को सीधे प्रभावित करती है। 32-बिट सिस्टम के युग में, यह संख्या कम्प्यूटेशनल शक्ति की सीमा का पर्याय थी। M_31 का मान अक्सर साधारण यादृच्छिक संख्या जनरेटर में मॉड्यूलस के रूप में भी कार्य करता था, क्योंकि अभाज्य होने के नाते, यह अच्छे सांख्यिकीय गुण प्रदान करता था। यह इस बात का एक स्पष्ट उदाहरण है कि कैसे एक अमूर्त गणितीय अवधारणा – एक मेर्सेन अभाज्य संख्या – व्यावहारिक इंजीनियरिंग में आधारशिला बन जाती है।

उच्च-लोड सिस्टम के विकास के व्यक्तिगत अनुभव से, मुझे याद है कि इस सीमा का अतिप्रवाह त्रुटियों का एक लगातार स्रोत था (यूनिक्स समय में तथाकथित Y2038 समस्या), जो इन गणितीय सीमाओं को समझने के व्यावहारिक महत्व को रेखांकित करता है।

GIMPS परियोजना क्या करती है और यह कैसे काम करती है?

GIMPS परियोजना नागरिक विज्ञान का एक प्रमुख उदाहरण है, जहां कोई भी एक महान गणितीय समस्या को हल करने के लिए अपने कंप्यूटर की कम्प्यूटेशनल शक्ति दान कर सकता है। परियोजना का संचालन एल्गोरिदम कार्यों के कुशल वितरण पर बनाया गया है:

1. केंद्रीय सर्वर प्रतिभागियों को अभाज्यता के उम्मीदवार देता है – संख्याओं M_p = 2^p – 1 के लिए विशिष्ट घातांक p।
2. क्लाइंट प्रोग्राम (Prime95 या mprime) पृष्ठभूमि में इस विशिष्ट मेर्सेन संख्या की अभाज्यता की जांच के लिए लुकास-लेहमर परीक्षण करता है।
3. यदि उम्मीदवार परीक्षण पास करता है, तो त्रुटियों को दूर करने के लिए परिणाम को दूसरे कंप्यूटर पर अलग सॉफ़्टवेयर और हार्डवेयर के साथ दोबारा जांचा जाता है।
4. दोहरी जांच के बाद, खोज की घोषणा की जाती है, और संख्या खोजने वाले प्रतिभागियों को एक मामूली नकद पुरस्कार (आमतौर पर लगभग $3,000) का हिस्सा और निश्चित रूप से, विश्वव्यापी प्रसिद्धि प्राप्त हो सकती है।

इस विकेंद्रीकृत मॉडल के कारण, GIMPS परियोजना ने वर्षों में मेर्सेन संख्याओं के लिए सभी संभावित घातांकों की एक विशाल श्रृंखला में जाँच की है, जो एक सुपर कंप्यूटर के लिए भी दुर्गम होगी। ऐसी परियोजनाओं में भाग लेने से न केवल विज्ञान को लाभ होता है, बल्कि स्थिरता के लिए अपने स्वयं के कंप्यूटर हार्डवेयर के तनाव परीक्षण का एक शानदार तरीका भी है।

मेर्सेन ट्विस्टर पर आधारित यादृच्छिक संख्या जनरेटर कैसे काम करता है?

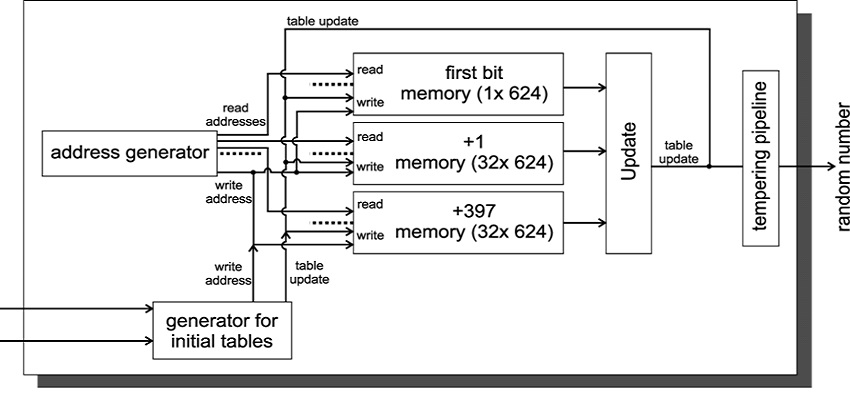
Mersenne Twister यादृच्छिक संख्या जनरेटर का संचालन एक आंतरिक अवस्था – 624 बत्तीस-बिट शब्दों की एक सरणी के साथ हेरफेर पर आधारित है। एल्गोरिदम को एक चक्रीय प्रक्रिया के रूप में कल्पना की जा सकती है जहाँ प्रत्येक चरण में इस सरणी से एक शब्द एक आउटपुट मूल्य प्राप्त करने के लिए बिटवाइज़ ऑपरेशन (शिफ्ट, एक्सक्लूसिव OR, गुणन) की एक श्रृंखला से गुजरता है।

सभी 624 शब्दों का उपयोग होने के बाद, अवस्था को एक विशेष मोड़ (twist) फ़ंक्शन का उपयोग करके “फेंटा” जाता है, जिसने एल्गोरिदम को उसका नाम दिया – “ट्विस्टर”। यह प्रक्रिया गारंटी देती है कि जनरेटर की अवधि सभी संभावित आंतरिक अवस्थाओं की गणना की अवधि के बराबर होगी, जिसे मेर्सेन अभाज्य संख्या M_19937 के बराबर चुना गया है।

नियतात्मकता इस तथ्य से सुनिश्चित होती है कि एक ही seed मान के साथ, सरणी समान रूप से आरंभ होती है, जिससे संख्याओं का समान अनुक्रम प्राप्त होता है। यह प्रोग्राम डीबगिंग के लिए अत्यंत महत्वपूर्ण है: यदि कोई सिमुलेशन अजीब व्यवहार करता है, तो डेवलपर त्रुटि खोजने के लिए बिल्कुल वही “यादृच्छिक” घटनाओं को पुनः बना सकता है।

इस एल्गोरिदम की ताकत और कमजोरियाँ क्या हैं?

किसी भी उपकरण की तरह, मेर्सेन ट्विस्टर के अपने इष्टतम अनुप्रयोग क्षेत्र हैं। इसके निर्विवाद लाभों में एक अत्यंत लंबी अवधि शामिल है, जो किसी भी व्यावहारिक गणना में अनुक्रम पुनरावृत्ति को समाप्त करती है, और यादृच्छिकता की उच्च गुणवत्ता है, जिसकी पुष्टि कई सांख्यिकीय परीक्षणों द्वारा की गई है। यह अधिकांश कार्यों के लिए पर्याप्त रूप से तेज़ भी है। हालाँकि, इसकी कमियाँ भी हैं। इनमें से मुख्य है बड़ी आंतरिक अवस्था (लगभग 2.5 KB), जो सीमित मेमोरी वाले सिस्टम, जैसे एम्बेडेड उपकरणों के लिए एक समस्या हो सकती है।

एल्गोरिदम अपेक्षाकृत धीमी आरंभीकरण (seed चयन) भी दिखाता है, जो जनरेटर के बार-बार पुनः आरंभ करने की आवश्यकता होने पर ध्यान देने योग्य हो सकता है। लेकिन सबसे गंभीर कमी, जिसका पहले ही उल्लेख किया जा चुका है, क्रिप्टोग्राफी के लिए इसकी अनुपयुक्तता है।

चूंकि एल्गोरिदम आउटपुट अनुक्रम में अपनी आंतरिक स्थिति को प्रकट करता है, 624 क्रमागत संख्याओं का अवलोकन करने के बाद, कोई पूरी तरह से स्थिति को पुनर्प्राप्त कर सकता है और सभी भविष्य के मूल्यों की भविष्यवाणी कर सकता है। गेम्स या वैज्ञानिक सिमुलेशन के लिए यह कोई समस्या नहीं है, लेकिन डेटा एन्क्रिप्शन के लिए यह एक महत्वपूर्ण दोष है।

कोड में मेर्सेन ट्विस्टर को सही ढंग से कैसे आरंभ और उपयोग करें?

उचित आरंभीकरण एक गुणवत्तापूर्ण यादृच्छिक अनुक्रम प्राप्त करने की कुंजी है। seed को एक स्थिरांक (उदाहरण के लिए, 0 या 1) में सरलता से सेट करने से प्रोग्राम हर बार चलने पर समान परिणाम देगा, जो पुनरुत्पादन क्षमता के लिए अच्छा है लेकिन, उदाहरण के लिए, ऑनलाइन गेम के लिए बुरा है। अक्सर सिस्टम के वर्तमान समय पर आधारित seed का उपयोग किया जाता है, लेकिन यह भी आदर्श नहीं है यदि प्रोग्राम को एक सेकंड में कई बार लॉन्च किया जाता है। आधुनिक कार्यान्वयन अधिक जटिल योजनाओं का उपयोग करने की सलाह देते हैं, उदाहरण के लिए, ओएस के विभिन्न स्रोतों से एन्ट्रॉपी एकत्र करना।

Python में, किसी दिए गए श्रेणी में एक पूर्णांक प्राप्त करने के लिए, `randint(a, b)` विधि का उपयोग करना चाहिए, न कि `random()` परिणाम के मॉड्यूलो को, क्योंकि बाद वाला वितरण में पूर्वाग्रह ला सकता है। किसी अनुक्रम से यादृच्छिक तत्व चुनने के लिए, `random.choice(seq)` का उपयोग करना अधिक सुरक्षित है। उच्च-लोड मल्टीथ्रेडेड अनुप्रयोगों में, यह सुनिश्चित करना आवश्यक है कि प्रत्येक थ्रेड का अपना जनरेटर उदाहरण हो, क्योंकि एक साझा वस्तु पहुंच सिंक्रनाइज़ेशन की आवश्यकता के कारण बोतलगले बन जाएगी।

मेर्सेन संख्याएँ और फर्माट संख्याएँ कैसे भिन्न हैं?

मेर्सेन संख्याएँ (M_n = 2^n – 1) और फर्माट संख्याएँ (F_n = 2^(2^n) + 1) संख्या सिद्धांत में दो प्रसिद्ध परिवार हैं, जिनमें से प्रत्येक महानतम गणितज्ञों और उनकी अद्वितीय समस्याओं से जुड़ा हुआ है। वे न केवल सूत्र में भिन्न हैं, बल्कि ऐतिहासिक संदर्भ, गुणों और अनुप्रयोग क्षेत्रों में भी भिन्न हैं। पियरे डे फर्माट ने अनुमान लगाया कि इस रूप की सभी संख्याएँ अभाज्य हैं, लेकिन, मेर्सेन के मामले की तरह, उनकी परिकल्पना गलत साबित हुई: ऑयलर ने F_5 के लिए एक भाजक पाया। आज तक, केवल पाँच फर्माट अभाज्य संख्याएँ ज्ञात हैं (F_0-F_4), और यह अनुमान है कि कोई अन्य नहीं हैं।

जबकि मेर्सेन अभाज्य संख्याएँ सम पूर्ण संख्याएँ उत्पन्न करती हैं, फर्माट अभाज्य संख्याओं का ज्यामिति के साथ गहरा संबंध है – वे परकार और रूलर से नियमित बहुभुज बनाने की समस्या में प्रकट होती हैं। गॉस-वांटज़ेल प्रमेय में कहा गया है कि एक नियमित n-गॉन का निर्माण तभी किया जा सकता है जब n दो की घात, एक फर्माट अभाज्य संख्या, या दो की घात और विभिन्न फर्माट अभाज्य संख्याओं का गुणनफल हो।

इस प्रकार, ये अमूर्त वस्तुएँ एक प्राचीनतम ज्यामितीय समस्या के समाधान को सीधे प्रभावित करती हैं।

आधुनिक दुनिया में फर्माट संख्याओं का उपयोग कहाँ किया जाता है?

मेर्सेन संख्याओं के विपरीत, जिन्होंने कंप्यूटिंग में व्यापक अनुप्रयोग पाया है, फर्माट संख्याओं की एक संकीर्ण लेकिन अत्यंत महत्वपूर्ण जगह है – क्रिप्टोग्राफी। विशेष रूप से, फर्माट अभाज्य संख्या F_4 = 65537 (2^16 + 1) RSA एल्गोरिदम में सार्वजनिक घातांक `e` के रूप में एक अविश्वसनीय रूप से लोकप्रिय विकल्प बन गई है।

इस चुनाव के कारण व्यावहारिक और सुंदर हैं: पहला, 65537 अभाज्य है, जो मॉड्यूलो φ(n) में प्रतिलोमता की गारंटी देता है; दूसरा, इसका द्विआधारी निरूपण केवल दो एक (10000000000000001) है, जो एक तेज़ एल्गोरिदम का उपयोग करके घातांक को बहुत कुशलता से लागू करने की अनुमति देता है जिसमें हजारों के बजाय केवल 17 गुणन संचालन की आवश्यकता होती है। यह सीमित कम्प्यूटेशनल शक्ति वाले उपकरणों पर एन्क्रिप्शन गति और डिजिटल हस्ताक्षर सत्यापन में एक महत्वपूर्ण लाभ प्रदान करता है, जैसे कि स्मार्ट कार्ड और मोबाइल फोन।

इस प्रकार, हर बार जब आप एक सुरक्षित ऑनलाइन लेनदेन करते हैं, तो आप संभवतः अनजाने में एक फर्माट संख्या का उपयोग कर रहे हैं।

विज्ञान और प्रौद्योगिकी के लिए इनमें से कौन सा संख्या परिवार अधिक महत्वपूर्ण है?

मेर्सेन और फर्माट संख्याओं के महत्व की तुलना करना पहिए और लीवर के महत्व की तुलना करने जैसा है। प्रत्येक परिवार अपने अद्वितीय कार्यों को हल करता है। मौलिक गणित और कंप्यूटेशनल विज्ञान के विकास के लिए, मेर्सेन संख्याओं ने निश्चित रूप से अधिक प्रभाव डाला है। वे पूर्ण संख्याओं से जुड़ी हुई हैं, अभाज्यता परीक्षण एल्गोरिदम के लिए परीक्षण मैदान के रूप में कार्य करती हैं, और सबसे लोकप्रिय यादृच्छिक संख्या जनरेटरों में से एक का आधार बनती हैं। उनकी खोज वितरित कंप्यूटिंग के विकास की प्रेरक शक्ति बन गई है।

दूसरी ओर, फर्माट संख्याओं ने अधिक विशिष्ट लेकिन गंभीर रूप से महत्वपूर्ण क्षेत्रों – ज्यामिति और क्रिप्टोग्राफी में अपनी नियति पाई है। एक विशिष्ट फर्माट संख्या (65537) प्रतिदिन ट्रिलियन डॉलर के वित्तीय लेनदेन की रक्षा करती है। इसलिए, उनके महत्व के प्रश्न का उत्तर संदर्भ पर निर्भर करता है: एक सिमुलेशन लिखने वाले प्रोग्रामर के लिए, मेर्सेन ट्विस्टर अधिक महत्वपूर्ण है; एक सुरक्षा प्रणाली विकसित करने वाले इंजीनियर के लिए, फर्माट संख्या महत्वपूर्ण है।

दोनों परिवार इस बात के शानदार उदाहरण हैं कि कैसे शुद्ध, अमूर्त गणित सदियों बाद प्रौद्योगिकी में महत्वपूर्ण अनुप्रयोग पाता है, उस दुनिया को आकार देता है जिसमें हम रहते हैं।

मेर्सेन अभाज्य संख्या की गणना तकनीकी विकास को कैसे प्रभावित करती है?

बड़े और बड़े मेर्सेन अभाज्य संख्याओं का पीछा करना रिकॉर्ड स्थापित करने के लिए केवल एक शैक्षणिक अभ्यास नहीं है। यह प्रक्रिया कई प्रमुख प्रौद्योगिकी क्षेत्रों में प्रगति के लिए एक उत्प्रेरक के रूप में कार्य करती है। सबसे पहले, यह बड़े पूर्णांकों के त्वरित गुणन के एल्गोरिदम, जैसे कि Schönhage-Strassen एल्गोरिदम या Fürer एल्गोरिदम में सुधार को बढ़ावा देती है, जो संख्या सिद्धांत से कहीं आगे – सिग्नल प्रोसेसिंग, कंप्यूटर ग्राफिक्स और क्रिप्टोग्राफी में अनुप्रयोग पाते हैं। दूसरा, दसियों लाख अंकों वाली संख्याओं की जाँच की आवश्यकता वितरित कंप्यूटिंग के लिए उच्च-प्रदर्शन सॉफ्टवेयर के निर्माण और अनुकूलन की माँग करती है।

GIMPS परियोजना और इसके क्लाइंट Prime95 प्रोसेसरों के तनाव परीक्षण और फ़्लोटिंग-पॉइंट अंकगणित में सबसे दुर्लभ त्रुटियों की पहचान के लिए मानक उपकरण बन गए हैं, जो सीधे उपभोक्ता हार्डवेयर की गुणवत्ता को प्रभावित करता है।

अंत में, ऐसी परियोजनाओं का संगठनात्मक मॉडल स्वयं अन्य नागरिक विज्ञान पहलों के लिए एक प्रोटोटाइप के रूप में कार्य करता है, अलौकिक संकेतों की खोज (SETI@home) से लेकर प्रोटीन फोल्डिंग (Folding@home) तक, सामूहिक बुद्धि और वितरित संसाधनों की शक्ति का प्रदर्शन करता है।

मेर्सेन अभाज्य संख्याओं की खोज में अगली सीमा क्या है?

इस शिकार में अगली बड़ी सीमा मेर्सेन अभाज्य संख्याओं की अनंतता की परिकल्पना का औपचारिक प्रमाण है। अनुभवजन्य साक्ष्य और अनुमानी तर्कों के बावजूद, इस तथ्य का कोई कठोर गणितीय प्रमाण अभी तक मौजूद नहीं है। इसकी खोज संख्या सिद्धांत में सदी की घटना होगी।

व्यावहारिक दृष्टि से, खोज नए रिकॉर्ड की ओर बढ़ती रहती है। प्रत्येक नई खोज के साथ, अगले उम्मीदवार की जाँच के लिए अधिक कम्प्यूटेशनल संसाधनों और समय की आवश्यकता होती है। यह नए एल्गोरिदमिक सफलताओं की आवश्यकता पैदा करता है, संभवतः क्वांटम कंप्यूटिंग या अभाज्यता परीक्षण के लिए मौलिक रूप से नए दृष्टिकोणों का उपयोग करके। यह भी संभावना है कि अगला रिकॉर्ड कृत्रिम बुद्धि की मदद से स्थापित किया जा सकता है, जो अभाज्य संख्याओं के वितरण में नए पैटर्न की खोज कर सकता है या खोज मापदंडों को अनुकूलित कर सकता है।

कोई फर्क नहीं पड़ता कि अगला सफलता कैसे प्राप्त की जाती है, यह निश्चित रूप से नई प्रौद्योगिकियों और विचारों को अपने साथ लाएगी जो गणित से कहीं आगे अनुप्रयोग पाएंगी, मेर्सेन, फर्माट और ऑयलर द्वारा शुरू की गई सदियों पुरानी परंपरा को जारी रखेंगी।