ไขปริศนาแห่งจักรวาล: คู่มือฉบับสมบูรณ์เกี่ยวกับทวิสเตอร์เมอร์เซนน์ ตัวเลข และผลกระทบต่อเทคโนโลยี

เมอร์เซนน์ ทวิสเตอร์ (Mersenne Twister) คืออัลกอริทึมที่นิยมและมีประสิทธิภาพมากสำหรับการสร้างตัวเลขสุ่มเทียม (PRNG) ซึ่งใช้ในคอมพิวเตอร์เพื่อสร้างลำดับที่เลียนแบบการสุ่ม เช่น ในเกม การจำลอง และสถิติ เป็นที่รู้จักจากคาบเวลาอันยาวนานมหาศาล (ลำดับจะเกิดซ้ำหลังจากตัวเลขจำนวนมากเพียง ~4.3×10^6001) ความเร็วในการสร้างสูง และคุณภาพทางสถิติที่ดี แต่ไม่เหมาะสำหรับการเข้ารหัสลับ เนื่องจากสามารถกู้คืนสถานะของมันได้หากมีตัวเลขที่สร้างแล้ว 624 ตัว

เมอร์เซนน์ ทวิสเตอร์ ไม่ใช่ปรากฏการณ์ทางกายภาพ แต่เป็นชื่อเชิงอุปมาที่ใช้ในคณิตศาสตร์และวิทยาการคอมพิวเตอร์เพื่ออธิบายอัลกอริทึมที่มีประสิทธิภาพสำหรับการสร้างตัวเลขสุ่มเทียม โดยอิงจากคุณสมบัติของจำนวนเฉพาะเมอร์เซนน์ อัลกอริทึมนี้ ซึ่งรู้จักกันในชื่อ เมอร์เซนน์ ทวิสเตอร์ หรือ Mersenne Twister มีคุณค่าอย่างยิ่งเนื่องจากคาบเวลาที่ยาวนานเป็นพิเศษ เท่ากับจำนวนเมอร์เซนน์ M_19937 ซึ่งหมายถึง 2^19937 – 1 และคุณภาพการกระจายตัวของตัวเลขสุ่มที่สูง

คุณค่าทางปฏิบัติของเมอร์เซนน์ ทวิสเตอร์อยู่ที่การนำไปใช้อย่างแพร่หลายสำหรับการสร้างแบบจำลอง การเข้ารหัสลับ (พร้อมข้อควรระวัง) เกมคอมพิวเตอร์ และการคำนวณทางวิทยาศาสตร์ ซึ่งจำเป็นต้องมีแหล่งสุ่มที่เชื่อถือได้ ความเข้าใจอัลกอริทึมนี้เชื่อมโยงอย่างแยกไม่ออกกับการศึกษาจำนวนเมอร์เซนน์เอง — ตัวเลขในรูปแบบ M_n = 2^n – 1 ซึ่งเป็นจำนวนเฉพาะภายใต้เงื่อนไขบางประการเท่านั้น และได้ทำให้นักคณิตศาสตร์หลงใหลมาหลายศตวรรษ

การค้นหาจำนวนเฉพาะเมอร์เซนน์ ซึ่งเป็นจำนวนเฉพาะที่รู้จักที่ใหญ่ที่สุด และความต้องการเครื่องสร้างตัวเลขสุ่มคุณภาพสูงสำหรับระบบคอมพิวเตอร์ นำไปสู่การสร้างอัลกอริทึมอันยอดเยี่ยมนี้ ซึ่งได้กลายเป็นมาตรฐานในภาษาการเขียนโปรแกรมและระบบต่าง ๆ มากมาย

เมอร์เซนน์ ทวิสเตอร์คืออะไรและทำไมจึงสำคัญนัก?

เมื่อพูดถึง เมอร์เซนน์ ทวิสเตอร์ มักหมายถึงอัลกอริทึมเฉพาะ — Mersenne Twister (MT19937) ซึ่งพัฒนาในปี 1997 โดยนักวิทยาศาสตร์ชาวญี่ปุ่น มาคาโตะ มัตสึโมโตะ และ ทาคุจิ นิชิมูระ ภารกิจหลักของอัลกอริทึมนี้คือการสร้างลำดับตัวเลขที่คล้ายกับการสุ่มมากที่สุด แต่ในขณะเดียวกันก็เป็นกระบวนการกำหนดได้อย่างสมบูรณ์และสามารถทำซ้ำได้เมื่อให้ค่าเริ่มต้น (seed) เดียวกัน

คุณสมบัตินี้มีความสำคัญอย่างยิ่งสำหรับการทดลองทางวิทยาศาสตร์ ซึ่งผลการจำลองต้องสามารถตรวจสอบได้ ต่างจากเครื่องสร้างเชิงเส้นตรงแบบง่าย ๆ ซึ่งมีคาบสั้นและสามารถให้ผลลัพธ์ที่คาดเดาได้ เมอร์เซนน์ ทวิสเตอร์ให้การกระจายตัวของตัวเลขที่สม่ำเสมอในหลายมิติสูงถึง 623 มิติ ทำให้มันเป็นหนึ่งในเครื่องสร้างที่เชื่อถือได้ที่สุดสำหรับการใช้งานทั่วไป

การพัฒนาของมันเป็นการตอบสนองต่อความต้องการที่เพิ่มขึ้นของคณิตศาสตร์เชิงคำนวณในช่วงกลางทศวรรษที่ 90 เมื่ออัลกอริทึมที่มีอยู่เดิมไม่สามารถจัดการกับงานการสร้างแบบจำลองระบบที่ซับซ้อนได้อีกต่อไป

คุณสมบัติหลักของอัลกอริทึม Mersenne Twister คืออะไร?

อัลกอริทึมเมอร์เซนน์ ทวิสเตอร์มีคุณลักษณะหลายประการที่ทำให้มันเป็นเครื่องมือที่ยอดเยี่ยม อย่างแรก คาบเวลาของมันใหญ่อย่างไม่น่าเชื่อ คือ 2^19937 – 1 ซึ่งเกินกว่าจำนวนอนุภาคมูลฐานในเอกภพ ตัวเลขนี้คือจำนวนเฉพาะเมอร์เซนน์ นี่คือที่มาของชื่ออัลกอริทึม อย่างที่สอง มันให้การกระจายตัวของค่าที่สม่ำเสมอทั่วทั้งพื้นที่สถานะของมัน ซึ่งได้รับการยืนยันโดยการทดสอบทางสถิติที่เข้มงวด เช่น การทดสอบ Diehard tests อย่างที่สาม มันถูกนำไปใช้อย่างมีประสิทธิภาพบนฮาร์ดแวร์คอมพิวเตอร์สมัยใหม่โดยใช้การดำเนินการแบบบิต และมีประสิทธิภาพที่ดี อย่างไรก็ตาม สิ่งสำคัญที่ต้องทราบคืออัลกอริทึมนี้ไม่ปลอดภัยทางด้านวิทยาการเข้ารหัสลับ: หากรู้ค่าผลลัพธ์ที่เรียงต่อเนื่องกันจำนวนหนึ่ง ก็สามารถกู้คืนสถานะภายในและทำนายลำดับทั้งหมดที่ตามมาได้ ดังนั้น สำหรับงานที่เกี่ยวข้องกับความปลอดภัย จึงใช้เครื่องสร้างเฉพาะทางอื่น ๆ

เมอร์เซนน์ ทวิสเตอร์ถูกใช้งานอย่างไรในแอปพลิเคชันจริง?

ด้วยคุณสมบัติของมัน เมอร์เซนน์ ทวิสเตอร์ได้กลายเป็นเครื่องสร้างตัวเลขสุ่มมาตรฐานในระบบยอดนิยมมากมาย ตัวอย่างเช่น มันเป็นเครื่องสร้างค่าเริ่มต้นในภาษาการเขียนโปรแกรม เช่น Python (โมดูล random), R, Ruby, PHP และแพ็คเกจคณิตศาสตร์ทั่วไปอย่าง MATLAB ในเกมคอมพิวเตอร์ มันมักถูกใช้เพื่อสร้างเลเวล เหตุการณ์ และพฤติกรรมของตัวละครที่ไม่ใช่ผู้เล่น สร้างประสบการณ์การเล่นเกมที่หลากหลายและในขณะเดียวกันก็สามารถทำซ้ำได้ ในการวิจัยทางวิทยาศาสตร์ โดยเฉพาะในวิธีมอนติคาร์โลสำหรับฟิสิกส์ การสร้างแบบจำลองทางการเงิน และชีวสารสนเทศ อัลกอริทึมนี้ให้ความสุ่มที่จำเป็นเพื่อให้ได้ผลลัพธ์ที่มีนัยสำคัญทางสถิติ

จากประสบการณ์ส่วนตัวในการทำงานกับโครงการแมชชีนเลิร์นนิง ข้าพเจ้าสามารถบอกได้ว่าการกำหนดค่าเริ่มต้นน้ำหนักของเครือข่ายประสาทเทียมมักขึ้นอยู่กับเครื่องสร้างตัวเลขสุ่มคุณภาพสูง และเมอร์เซนน์ ทวิสเตอร์เป็นตัวเลือกที่เชื่อถือได้สำหรับงานนี้มาเป็นเวลานาน จนกระทั่งมีวิธีการเฉพาะทางมากขึ้นปรากฏขึ้น

วิธีการกำหนดค่าเริ่มต้นและใช้งานเมอร์เซนน์ ทวิสเตอร์ในการเทรดและการลงทุนอย่างถูกต้อง?

การกำหนดค่าเริ่มต้นและการใช้ เมอร์เซนน์ ทวิสเตอร์ ในการสร้างแบบจำลองทางการเงิน การเทรดด้วยอัลกอริทึม และการประเมินความเสี่ยงในการลงทุน ต้องการความใส่ใจเป็นพิเศษต่อความแน่นอน (determinism) และคุณภาพของความสุ่ม

หลักการสำคัญคือ ความสามารถในการทำซ้ำผลลัพธ์ของการแบ็กเทสต์กลยุทธ์การเทรดได้อย่างรับประกัน เพื่อให้บรรลุสิ่งนี้ ค่าเริ่มต้น (seed) ของเครื่องสร้างต้องถูกกำหนดไว้อย่างชัดเจนในโค้ดเป็นค่าคงที่ แทนที่จะขึ้นอยู่กับเวลาปัจจุบันของระบบ สิ่งนี้ทำให้สามารถสร้างลำดับทั้งหมดของเหตุการณ์ “สุ่ม” ขึ้นมาใหม่ได้อย่างแม่นยำ — การกระชากของราคา, เวลาการดำเนินการออเดอร์ — และทำให้มั่นใจว่ากำไรของกลยุทธ์มีความเสถียรในการรันทดสอบหลายครั้ง แทนที่จะเป็นผลมาจากการจำลองที่โชคดีเพียงครั้งเดียว

ในระบบการเทรดที่มีโหลดสูงซึ่งประมวลผลสตรีมข้อมูลหลายสตรีม แต่ละโมดูลเชิงตรรกะ (เช่น ตัวจำลองผลกระทบของตลาด, เครื่องสร้างพารามิเตอร์สำหรับการปรับให้เหมาะสม, และโมดูลการประเมินความเสี่ยง) ควรใช้อินสแตนซ์เครื่องสร้างของตัวเองที่แยกออกมาต่างหาก โดยมี seed ที่ไม่ซ้ำกัน แต่ก็ยังเป็น deterministic เช่นกัน สิ่งนี้ป้องกันไม่ให้มีความสัมพันธ์โดยนัยระหว่างกระบวนการสุ่ม ซึ่งอาจบิดเบือนสถิติสุดท้าย เช่น การขาดทุนสูงสุด (maximum drawdown) หรืออัตราส่วน Sharpe

สำหรับการสร้างแบบจำลองเส้นทางการเคลื่อนที่ของราคาสินทรัพย์ ตัวอย่างเช่น ใช้วิธีมอนติคาร์โลสำหรับการกำหนดราคาออปชันหรือ Value at Risk (VaR) การเรียกการกระจายตัวสม่ำเสมอ `random()` แบบมาตรฐานมักไม่เพียงพอ จำเป็นต้องแปลงลำดับที่กระจายสม่ำเสมอจากเมอร์เซนน์ ทวิสเตอร์เป็นการกระจายทางสถิติอื่น ๆ เช่น การแจกแจงปกติหรือล็อกนอร์มัล โดยใช้อัลกอริทึมเช่น การแปลงแบบบ็อกซ์-มิวเลอร์ ในเวลาเดียวกัน สิ่งสำคัญอย่างยิ่งคือต้องตระหนักถึงและชดเชยจุดด้อยหลักของอัลกอริทึมสำหรับแวดวงการเงิน นั่นคือความสามารถในการทำนายได้เมื่อสังเกตลำดับผลลัพธ์ที่ยาวพอ

แม้ว่าสำหรับจุดประสงค์การแบ็กเทสต์เพื่อการวิจัยล้วน ๆ นี่จะไม่ใช่ปัญหา แต่สำหรับการทำงานของระบบการเทรดสด ซึ่งความสุ่มอาจถูกใช้เพื่อทำให้เวลาการส่งออเดอร์เป็นแบบสุ่ม ปัจจัยนี้เป็นช่องโหว่ทางทฤษฎี ดังนั้น ในสภาพแวดล้อมการทำงานจริง โดยเฉพาะในการเทรดความถี่สูง มักใช้แนวทางแบบไฮบริด ซึ่งเมอร์เซนน์ ทวิสเตอร์ที่กำหนดค่าเริ่มต้นด้วย seed ทางวิทยาการเข้ารหัสลับที่ปลอดภัย จะถูกผสมรวมกับแหล่งเอนโทรปีจริงจากเครื่องสร้างตัวเลขสุ่มทางฮาร์ดแวร์ เพื่อปรับปรุงสถานะเป็นระยะ

ตัวอย่างปฏิบัติจากประสบการณ์การจัดการความเสี่ยง: เมื่อคำนวณ VaR สำหรับพอร์ตโฟลิโอโดยใช้การจำลองทางประวัติศาสตร์ด้วยวิธีมอนติคาร์โล เราได้สร้างสถานการณ์ราคาในอนาคตหลายแสนสถานการณ์ การใช้เมอร์เซนน์ ทวิสเตอร์กับ seed ที่คงที่ในช่วงพัฒนารูปแบบ ทำให้ทีมนักวิเคราะห์ทั้งหมดสามารถทำงานกับข้อมูลที่เหมือนกันและทดสอบผลกระทบของปัจจัยใหม่ ๆ อย่างสม่ำเสมอ อย่างไรก็ตาม ในรายงานสุดท้ายสำหรับหน่วยงานกำกับดูแล seed จะถูกเปลี่ยน และการคำนวณทั้งหมดจะถูกทำซ้ำหนึ่งพันครั้งเพื่อให้ได้ช่วงความเชื่อมั่นสำหรับตัวชี้วัด VaR เอง ซึ่งแสดงให้เห็นถึงความแข็งแกร่งของโมเดล

แนวทางสองขั้นตอนนี้ — ความแน่นอน (determinism) สำหรับการพัฒนาและการตรวจสอบ บวก ความแปรผันสำหรับการประเมินขั้นสุดท้าย — เป็นแนวปฏิบัติที่ดี มันยังช่วยหลีกเลี่ยงการ “โอเวอร์ฟิต” กลยุทธ์การเทรดให้เข้ากับลำดับสุ่มเฉพาะ: หากกลยุทธ์แสดงผลกำไรบน seed ที่กำหนดไว้ล่วงหน้าเพียงตัวเดียว แต่ “ล้มเหลว” บนอีกเป็นร้อยตัว นี่เป็นสัญญาณที่ชัดเจนของความไม่มีนัยสำคัญทางสถิติและการปรับเส้นโค้งให้เข้ากับสัญญาณรบกวน

ดังนั้น เมอร์เซนน์ ทวิสเตอร์จึงทำหน้าที่เป็นเครื่องมือที่เชื่อถือได้และมีประสิทธิภาพในการเงิน เพื่อสร้างสภาพแวดล้อมเชิงสุ่มแบบควบคุมได้ การใช้งานที่เหมาะสมของมันสร้างขึ้นบนหลักการสามประการ: ความแน่นอน (determinism) ที่เข้มงวดเพื่อความสามารถในการทำซ้ำของการทดสอบ, การแยกเครื่องสร้างเพื่อความบริสุทธิ์ของการทดลอง, และการเปลี่ยนไปสู่ความแปรผันและแหล่งสุ่มที่ปลอดภัยทางวิทยาการเข้ารหัสลับอย่างมีสติในขั้นตอนการวิเคราะห์สุดท้ายและในระบบปฏิบัติการ อัลกอริทึมนี้ช่วยเปลี่ยนความไม่แน่นอนของตลาดให้เป็นความเสี่ยงและโอกาสที่สามารถวัดได้เชิงปริมาณ ทำให้มั่นใจในความเข้มงวดทางคณิตศาสตร์ในการตัดสินใจลงทุน

ทำไมจึงต้องการจำนวนเมอร์เซนน์ และอะไรทำให้มันพิเศษ?

จำนวนเมอร์เซนน์ ซึ่งตั้งชื่อตามนักบวชชาวฝรั่งเศสในศตวรรษที่ 17 มาริน เมอร์เซนน์ มีรูปแบบ M_n = 2^n – 1 การศึกษาพวกมันไม่ได้เกิดจากความอยากรู้อยากเห็นเชิงนามธรรม แต่เกิดจากการเชื่อมโยงพื้นฐานกับทฤษฎีจำนวนและการประยุกต์ใช้เชิงปฏิบัติ

จำนวนเฉพาะเมอร์เซนน์เชื่อมโยงโดยตรงกับจำนวนสมบูรณ์ — ตัวเลขที่เท่ากับผลรวมของตัวหารแท้ของมัน ตามทฤษฎีบทที่พิสูจน์โดยยุคลิดและต่อมาสมบูรณ์โดยออยเลอร์ จำนวนสมบูรณ์คู่ทุกจำนวนสามารถแสดงเป็น 2^(p-1) * (2^p – 1) โดยที่ (2^p – 1) คือจำนวนเฉพาะเมอร์เซนน์

ความเชื่อมโยงอันลึกซึ้งนี้ทำให้พวกมันเป็นกุญแจสำคัญในการทำความเข้าใจโครงสร้างของจำนวนสมบูรณ์ นอกจากนี้ จำนวนเฉพาะเมอร์เซนน์ยังทำหน้าที่เป็นสนามทดสอบสำหรับอัลกอริทึมใหม่ ๆ ในการทดสอบความเป็นจำนวนเฉพาะและระบบคอมพิวเตอร์ที่มีประสิทธิภาพสูง ดังเช่นในโครงการ GIMPS (Great Internet Mersenne Prime Search) เนื่องจากธรรมชาติแบบไบนารีของพวกมัน (ลำดับต่อเนื่องของเลข 1 ในระบบไบนารี) พวกมันยังมีความสำคัญในวิทยาศาสตร์คอมพิวเตอร์ด้วย ตัวอย่างเช่น ในการสร้างรหัสที่แก้ไขข้อผิดพลาด

ประวัติศาสตร์เบื้องหลังการค้นหาจำนวนเฉพาะเมอร์เซนน์คืออะไร?

การตามล่าหาจำนวนเฉพาะเมอร์เซนน์เป็นตำนานหลายศตวรรษที่เต็มไปด้วยความผิดพลาด ชัยชนะ และความก้าวหน้าทางเทคโนโลยี เมอร์เซนน์เองในปี 1644 ได้กล่าวอ้างว่าค่า n ใดบ้างจนถึง 257 ที่ให้จำนวนเฉพาะ และการคาดเดาของเขาหลายอย่างกลับกลายเป็นว่าไม่ถูกต้อง การค้นหาเร่งขึ้นก็ต่อเมื่อมีการพัฒนาอุปกรณ์ทางคณิตศาสตร์และกำเนิดของคอมพิวเตอร์

เหตุการณ์สำคัญคือการค้นพบจำนวน M_1398269 ในปี 1996 โดยกำลังของโครงการ GIMPS ซึ่งใช้การคำนวณแบบกระจายจากอาสาสมัครหลายพันคนทั่วโลก การค้นพบใหม่ ๆ ของจำนวนเฉพาะที่รู้จักที่ใหญ่ที่สุดเกือบทุกครั้งเป็นจำนวนเมอร์เซนน์เสมอ ซึ่งบ่งบอกถึงประสิทธิภาพของอัลกอริทึมการตรวจสอบเฉพาะทาง เช่น การทดสอบลูคัส-เลห์เมอร์ การทดสอบนี้ พัฒนาขึ้นในทศวรรษ 1930 ทำให้สามารถตรวจสอบความเป็นจำนวนเฉพาะของจำนวนเมอร์เซนน์ได้ค่อนข้างรวดเร็ว (โดยมาตรฐานทฤษฎีจำนวน) โดยไม่ต้องทำการหารด้วยตัวหารที่เป็นไปได้ทั้งหมดอย่างยากลำบาก ตั้งแต่ปี 1952 เป็นต้นมา จำนวนเฉพาะที่ทำลายสถิติทั้งหมดถูกพบในหมู่จำนวนเมอร์เซนน์

การประยุกต์ใช้จำนวนเมอร์เซนน์ในทางปฏิบัติในปัจจุบันมีอะไรบ้าง?

• วิทยาการเข้ารหัสลับ: แม้ว่าจำนวนเมอร์เซนน์เองจะไม่ใช่พื้นฐานของระบบการเข้ารหัสลับสมัยใหม่ (เช่น RSA) แต่พวกมันถูกใช้เพื่อสร้างจำนวนเฉพาะขนาดใหญ่ที่จำเป็นในโปรโตคอลบางอย่าง เนื่องจากประสิทธิภาพของการทดสอบลูคัส-เลห์เมอร์
• การทดสอบฮาร์ดแวร์คอมพิวเตอร์: การดำเนินการกับจำนวนเมอร์เซนน์ขนาดมหึมาทำหน้าที่เป็นแบบทดสอบความเครียดสำหรับโปรเซสเซอร์และระบบหน่วยความจำ เปิดเผยข้อผิดพลาดในการคำนวณเลขทศนิยมและเลขคณิตจำนวนเต็ม
• ทฤษฎีการเข้ารหัส: โครงสร้างไบนารีของพวกมัน (เช่น M_3 = 7 ซึ่งคือ 111 ในระบบไบนารี) มีการประยุกต์ใช้ในการสร้างรหัสแบบไซคลิกและรูปแบบอื่น ๆ ที่แก้ไขข้อผิดพลาดในการส่งข้อมูล
• การวิจัยทางคณิตศาสตร์: พวกมันยังคงเป็นวัตถุศูนย์กลางในปัญหาที่ยังไม่ได้รับการแก้ไข เช่น สมมติฐานเกี่ยวกับจำนวนอนันต์ของจำนวนเฉพาะเมอร์เซนน์ การแก้ปัญหาซึ่งจะก้าวหน้าไปข้างหน้าทั้งทฤษฎีจำนวน

จำนวนเมอร์เซนน์ที่สำคัญที่สุด: อันไหนและเพราะเหตุใด?

ผู้สมควรหลายรายแข่งขันกันเพื่อตำแหน่ง จำนวนเมอร์เซนน์ ที่สำคัญที่สุด ขึ้นอยู่กับเกณฑ์ — ความสำคัญทางประวัติศาสตร์, ความงามทางคณิตศาสตร์, หรือความสำเร็จด้านการคำนวณ โดยทางรูปแบบแล้ว สิ่งที่สำคัญที่สุดในปัจจุบันคือจำนวนเฉพาะที่รู้จักที่ใหญ่ที่สุด ซึ่งณ ปี 2026 ก็คือจำนวนเฉพาะเมอร์เซนน์เช่นกัน สถิติล่าสุดที่ตั้งขึ้นภายในโครงการ GIMPS คือจำนวน M_82589933 ซึ่งมีตัวเลขฐานสิบเกือบ 25 ล้านหลัก

อย่างไรก็ตาม จากมุมมองทางประวัติศาสตร์และมโนทัศน์ จำนวน M_31 = 2^31 – 1 = 2147483647 มีบทบาทสำคัญอย่างมาก จำนวนนี้เป็นจำนวนเฉพาะเมอร์เซนน์และเป็นจำนวนเฉพาะที่รู้จักที่ใหญ่ที่สุดเป็นเวลานาน ซึ่งพบโดยเลออนฮาร์ด ออยเลอร์ในปี 1772 แต่ที่สำคัญยิ่งกว่านั้น M_31 คือค่าสูงสุดสำหรับจำนวนเต็มแบบมีเครื่องหมาย 32 บิตในวิทยาการคอมพิวเตอร์ ทำให้มันเป็นค่าคงที่พื้นฐานในการเขียนโปรแกรม กำหนดขอบเขตของอาร์เรย์, ตัวระบุ, และตัวเลขสุ่ม เครื่องสร้างตัวเลขสุ่มยุคแรก ๆ มากมาย รวมถึงเมอร์เซนน์ ทวิสเตอร์ ได้รับการพัฒนาด้วยขีดจำกัดของสถาปัตยกรรมโปรเซสเซอร์นี้ในใจ

M_31 มีอิทธิพลต่อการพัฒนาวิทยาการคอมพิวเตอร์อย่างไร?

จำนวน 2^31 – 1 ซึมซาบเข้าไปในรากฐานของการออกแบบซอฟต์แวร์ มันกำหนดช่วงบวกสูงสุดสำหรับประเภทข้อมูล `int32_t` ในภาษา C และ C++ ซึ่งส่งผลโดยตรงต่อการออกแบบโครงสร้างข้อมูล การจัดทำดัชนีอาร์เรย์ และการสร้างตัวระบุที่ไม่ซ้ำกัน ในยุคของระบบ 32 บิต จำนวนนี้เป็นคำพ้องความหมายของขีดจำกัดของพลังการคำนวณ ค่า M_31 มักทำหน้าที่เป็นมอดุลัสในเครื่องสร้างตัวเลขสุ่มแบบง่าย ๆ ด้วย เนื่องจากมันเป็นจำนวนเฉพาะ จึงให้คุณสมบัติทางสถิติที่ดี นี่เป็นตัวอย่างที่ชัดเจนของแนวคิดทางคณิตศาสตร์เชิงนามธรรม — จำนวนเฉพาะเมอร์เซนน์ — กลายเป็นรากฐานสำคัญในวิศวกรรมเชิงปฏิบัติ

จากประสบการณ์ส่วนตัวในการพัฒนาระบบที่มีโหลดสูง ข้าพเจ้าจำได้ว่าการล้น (overflow) ของขีดจำกัดนี้เป็นแหล่งที่มาของข้อผิดพลาดบ่อยครั้ง (ปัญหาที่เรียกว่า Y2038 problem ในเวลา Unix) ซึ่งเน้นย้ำถึงความสำคัญในทางปฏิบัติของการทำความเข้าใจข้อจำกัดทางคณิตศาสตร์เหล่านี้

โครงการ GIMPS ทำอะไรและทำงานอย่างไร?

โครงการ GIMPS เป็นตัวอย่างที่ชัดเจนของวิทยาศาสตร์พลเมือง ซึ่งทุกคนสามารถบริจาคพลังการคำนวณของคอมพิวเตอร์ของตนเพื่อแก้ปัญหาทางคณิตศาสตร์ที่ยิ่งใหญ่ อัลกอริทึมการทำงานของโครงการสร้างขึ้นจากการกระจายงานอย่างมีประสิทธิภาพ:

1. เซิร์ฟเวอร์กลางให้ผู้เข้าร่วมผู้สมควรสำหรับการทดสอบความเป็นจำนวนเฉพาะ — เลขชี้กำลัง p เฉพาะสำหรับจำนวน M_p = 2^p – 1
2. โปรแกรมไคลเอนต์ (Prime95 หรือ mprime) ดำเนินการทดสอบลูคัส-เลห์เมอร์ในพื้นหลังเพื่อตรวจสอบความเป็นจำนวนเฉพาะของจำนวนเมอร์เซนน์เฉพาะนี้
3. หากผู้สมควรผ่านการทดสอบ ผลลัพธ์จะถูกตรวจสอบซ้ำบนคอมพิวเตอร์เครื่องอื่นด้วยซอฟต์แวร์และฮาร์ดแวร์ที่แตกต่างกันเพื่อตัดข้อผิดพลาดออก
4. หลังจากการตรวจสอบสองครั้ง การค้นพบจะได้รับการประกาศ และผู้เข้าร่วมที่พบจำนวนอาจได้รับส่วนแบ่งของรางวัลเงินสดเล็กน้อย (โดยปกติประมาณ 3,000 ดอลลาร์) และแน่นอน ชื่อเสียงระดับโลก

ต้องขอบคุณโมเดลแบบกระจายอำนาจนี้ โครงการ GIMPS ตลอดหลายปีได้ตรวจสอบเลขชี้กำลังที่เป็นไปได้ทั้งหมดสำหรับจำนวนเมอร์เซนน์ในช่วงกว้างใหญ่ ซึ่งจะเข้าไม่ถึงแม้กระทั่งซูเปอร์คอมพิวเตอร์ การมีส่วนร่วมในโครงการดังกล่าวไม่เพียงแต่เป็นประโยชน์ต่อวิทยาศาสตร์ แต่ยังเป็นวิธีที่ยอดเยี่ยมในการทดสอบความเครียดฮาร์ดแวร์คอมพิวเตอร์ของตัวเองเพื่อหาความเสถียร

เครื่องสร้างตัวเลขสุ่มที่ใช้เมอร์เซนน์ ทวิสเตอร์ทำงานอย่างไร?

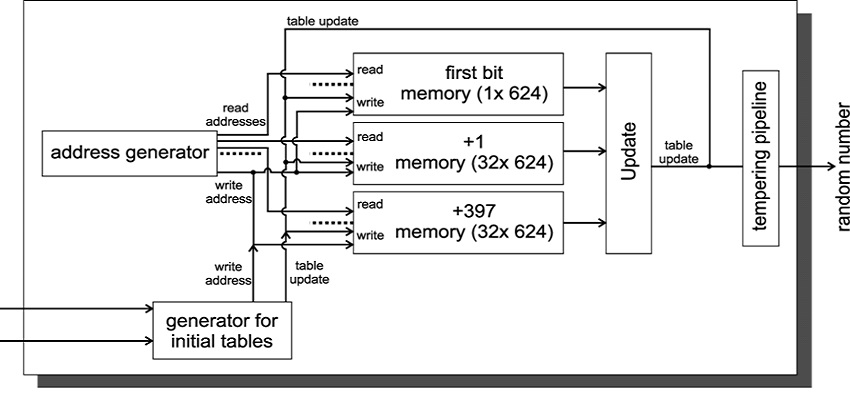
การทำงานของเครื่องสร้างตัวเลขสุ่ม Mersenne Twister ใช้การจัดการสถานะภายใน — อาร์เรย์ของคำ 32 บิตจำนวน 624 คำ อัลกอริทึมสามารถจินตนาการเป็นกระบวนการแบบวนซ้ำ โดยในแต่ละขั้นตอน คำหนึ่งจากอาร์เรย์นี้จะได้รับการดำเนินการแบบบิตเป็นชุด (การเลื่อน, exclusive OR, การคูณ) เพื่อสร้างค่าผลลัพธ์

หลังจากใช้คำทั้งหมด 624 คำแล้ว สถานะจะถูก “ปั่น” โดยใช้ฟังก์ชันบิด (twist) พิเศษ ซึ่งเป็นที่มาของชื่ออัลกอริทึม — “ทวิสเตอร์” กระบวนการนี้รับประกันว่าคาบเวลาของเครื่องสร้างจะเท่ากับคาบเวลาของการแจกแจงสถานะภายในที่เป็นไปได้ทั้งหมด ซึ่งถูกเลือกให้เท่ากับจำนวนเฉพาะเมอร์เซนน์ M_19937

ความแน่นอน (determinism) ได้รับการรับประกันโดยข้อเท็จจริงที่ว่าเมื่อมีค่า seed เดียวกัน อาร์เรย์จะถูกกำหนดค่าเริ่มต้นเหมือนกัน นำไปสู่ลำดับของตัวเลขเดียวกัน สิ่งนี้สำคัญอย่างยิ่งสำหรับการดีบักโปรแกรม: หากการจำลองทำงานแปลก ๆ นักพัฒนาสามารถสร้างเหตุการณ์ “สุ่ม” ที่แน่นอนเดียวกันขึ้นมาใหม่เพื่อค้นหาข้อผิดพลาด

จุดแข็งและจุดอ่อนของอัลกอริทึมนี้คืออะไร?

เช่นเดียวกับเครื่องมือใด ๆ เมอร์เซนน์ ทวิสเตอร์มีพื้นที่การใช้งานที่เหมาะสมที่สุด จุดแข็งที่ไม่อาจโต้แย้งได้ของมันรวมถึงคาบเวลาที่ยาวนานอย่างยิ่ง ซึ่งไม่รวมการเกิดซ้ำของลำดับในการคำนวณเชิงปฏิบัติใด ๆ และคุณภาพของความสุ่มที่สูง ซึ่งได้รับการยืนยันโดยการทดสอบทางสถิติมากมาย มันยังเร็วเพียงพอสำหรับงานส่วนใหญ่ อย่างไรก็ตาม มันก็มีข้อเสียเช่นกัน ข้อเสียหลักคือสถานะภายในที่ใหญ่ (เกือบ 2.5 KB) ซึ่งอาจเป็นปัญหาได้สำหรับระบบที่มีหน่วยความจำจำกัด เช่น อุปกรณ์ฝังตัว

อัลกอริทึมยังแสดงให้เห็นถึงการกำหนดค่าเริ่มต้น (การเลือก seed) ที่ค่อนข้างช้า ซึ่งอาจสังเกตเห็นได้เมื่อจำเป็นต้องรีสตาร์ตเครื่องสร้างบ่อยครั้ง แต่ข้อเสียที่ร้ายแรงที่สุด ซึ่งได้กล่าวถึงไปแล้ว คือความไม่เหมาะสมสำหรับวิทยาการเข้ารหัสลับ

เนื่องจากอัลกอริทึมเปิดเผยสถานะภายในของมันในลำดับผลลัพธ์ หลังจากการสังเกตตัวเลข 624 ตัวที่เรียงต่อเนื่องกัน เราสามารถกู้คืนสถานะและทำนายค่าทั้งหมดในอนาคตได้ สำหรับเกมหรือการจำลองทางวิทยาศาสตร์ นี่ไม่ใช่ปัญหา แต่สำหรับการเข้ารหัสข้อมูล นี่เป็นข้อบกพร่องที่สำคัญ

วิธีการกำหนดค่าเริ่มต้นและใช้งานเมอร์เซนน์ ทวิสเตอร์ในโค้ดอย่างถูกต้อง?

การกำหนดค่าเริ่มต้นที่เหมาะสมคือกุญแจสำคัญในการได้รับลำดับสุ่มที่มีคุณภาพ การตั้งค่า seed เป็นค่าคงที่อย่างง่าย (เช่น 0 หรือ 1) จะทำให้โปรแกรมให้ผลลัพธ์เดียวกันทุกครั้งที่รัน ซึ่งดีสำหรับความสามารถในการทำซ้ำ แต่ไม่ดีสำหรับ ตัวอย่างเช่น เกมออนไลน์ มักใช้ seed ที่อิงตามเวลาปัจจุบันของระบบ แต่สิ่งนี้ก็ยังไม่สมบูรณ์แบบหากโปรแกรมถูกละหลายครั้งภายในหนึ่งวินาที การใช้งานสมัยใหม่แนะนำให้ใช้โครงร่างที่ซับซ้อนกว่านี้ ตัวอย่างเช่น การรวบรวมเอนโทรปีจากแหล่งต่าง ๆ ของระบบปฏิบัติการ

ใน Python เพื่อให้ได้จำนวนเต็มในช่วงที่กำหนด ควรใช้เมธอด `randint(a, b)` มากกว่าการนำมอดุลัสของผลลัพธ์ `random()` เนื่องจากวิธีหลังอาจนำอคติเข้ามาในการกระจายตัว สำหรับการเลือกองค์ประกอบสุ่มจากลำดับ การใช้ `random.choice(seq)` จะปลอดภัยกว่า ในแอปพลิเคชันแบบมัลติเธรดที่มีโหลดสูง จำเป็นต้องทำให้แต่ละเธรดมีอินสแตนซ์เครื่องสร้างของตัวเอง เนื่องจากวัตถุที่ใช้ร่วมกันจะกลายเป็นคอขวดเนื่องจากความจำเป็นในการซิงโครไนซ์การเข้าถึง

จำนวนเมอร์เซนน์และจำนวนแฟร์มาต์แตกต่างกันอย่างไร?

จำนวนเมอร์เซนน์ (M_n = 2^n – 1) และ จำนวนแฟร์มาต์ (F_n = 2^(2^n) + 1) เป็นสองตระกูลที่มีชื่อเสียงในทฤษฎีจำนวน แต่ละตระกูลเกี่ยวข้องกับนักคณิตศาสตร์ผู้ยิ่งใหญ่และปัญหาที่เป็นเอกลักษณ์ของตัวเอง พวกมันแตกต่างกันไม่เพียงแต่ในสูตร แต่ยังรวมถึงบริบททางประวัติศาสตร์ คุณสมบัติ และพื้นที่การประยุกต์ใช้ ปีแยร์ เดอ แฟร์มาต์ตั้งสมมติฐานว่าจำนวนทั้งหมดในรูปแบบนี้เป็นจำนวนเฉพาะ แต่เช่นเดียวกับกรณีของเมอร์เซนน์ สมมติฐานของเขากลับกลายเป็นว่าผิด: ออยเลอร์พบตัวหารสำหรับ F_5 จนถึงทุกวันนี้ รู้จักจำนวนเฉพาะแฟร์มาต์เพียงห้าจำนวนเท่านั้น (F_0-F_4) และมีการคาดเดาว่าไม่มีจำนวนอื่นอีก

ในขณะที่จำนวนเฉพาะเมอร์เซนน์สร้างจำนวนสมบูรณ์คู่ จำนวนเฉพาะแฟร์มาต์มีความเชื่อมโยงอย่างลึกซึ้งกับเรขาคณิต — พวกมันปรากฏในปัญหาของการสร้างรูปหลายเหลี่ยมปรกติด้วยวงเวียนและเส้นตรง ทฤษฎีบทของเกาส์-วันต์เซลล์ระบุว่ารูป n เหลี่ยมปรกติสามารถสร้างได้ก็ต่อเมื่อ n เป็นกำลังของสอง, จำนวนเฉพาะแฟร์มาต์, หรือผลคูณของกำลังของสองและจำนวนเฉพาะแฟร์มาต์ที่แตกต่างกัน

ดังนั้น วัตถุเชิงนามธรรมเหล่านี้จึงส่งผลโดยตรงต่อการแก้ปัญหาทางเรขาคณิตที่เก่าแก่ที่สุด

จำนวนแฟร์มาต์ถูกนำไปใช้ในโลกสมัยใหม่อย่างไร?

แตกต่างจากจำนวนเมอร์เซนน์ซึ่งพบการประยุกต์ใช้อย่างกว้างขวางในการคำนวณ จำนวนแฟร์มาต์มีช่องเฉพาะที่แคบกว่าแต่สำคัญอย่างยิ่ง — วิทยาการเข้ารหัสลับ โดยเฉพาะอย่างยิ่ง จำนวนเฉพาะแฟร์มาต์ F_4 = 65537 (2^16 + 1) ได้กลายเป็นตัวเลือกที่นิยมอย่างไม่น่าเชื่อสำหรับเลขชี้กำลังสาธารณะ `e` ในอัลกอริทึม RSA

เหตุผลของการเลือกนี้เป็นไปในทางปฏิบัติและสง่างาม: อย่างแรก 65537 เป็นจำนวนเฉพาะ ซึ่งรับประกันความสามารถในการผกผันแบบมอดุโล φ(n); อย่างที่สอง การแสดงแบบไบนารีของมันมีเพียงสองหนึ่ง (10000000000000001) ซึ่งทำให้สามารถดำเนินการยกกำลังได้อย่างมีประสิทธิภาพมากโดยใช้อัลกอริทึมแบบเร็วที่ต้องการการดำเนินการคูณเพียง 17 ครั้งแทนที่จะเป็นหลายพันครั้ง สิ่งนี้ให้ผลกำไรอย่างมีนัยสำคัญในความเร็วของการเข้ารหัสและการตรวจสอบลายเซ็นดิจิทัลบนอุปกรณ์ที่มีพลังการคำนวณจำกัด เช่น สมาร์ทการ์ดและโทรศัพท์มือถือ

ดังนั้น ทุกครั้งที่คุณทำธุรกรรมออนไลน์ที่ปลอดภัย คุณมักจะใช้จำนวนแฟร์มาต์โดยไม่รู้ตัว

ตระกูลตัวเลขใดในสองตระกูลนี้สำคัญกว่าสำหรับวิทยาศาสตร์และเทคโนโลยี?

การเปรียบเทียบความสำคัญของจำนวนเมอร์เซนน์และจำนวนแฟร์มาต์ ก็เหมือนกับการเปรียบเทียบความสำคัญของล้อและคาน แต่ละตระกูลแก้ปัญหาเฉพาะของตัวเอง สำหรับการพัฒนาคณิตศาสตร์พื้นฐานและวิทยาศาสตร์คอมพิวเตอร์ จำนวนเมอร์เซนน์มีอิทธิพลอย่างแน่นอนมากกว่า พวกมันเชื่อมโยงกับจำนวนสมบูรณ์ ทำหน้าที่เป็นสนามทดสอบสำหรับอัลกอริทึมการทดสอบความเป็นจำนวนเฉพาะ และเป็นรากฐานของเครื่องสร้างตัวเลขสุ่มยอดนิยมตัวหนึ่ง การค้นหาพวกมันเป็นแรงขับเคลื่อนสำหรับการพัฒนาการคำนวณแบบกระจาย

ในทางกลับกัน จำนวนแฟร์มาต์พบชะตากรรมของพวกมันในสาขาที่เฉพาะทางแต่สำคัญอย่างยิ่ง — เรขาคณิตและวิทยาการเข้ารหัสลับ จำนวนแฟร์มาต์เฉพาะตัวหนึ่ง (65537) ปกป้องธุรกรรมทางการเงินมูลค่าล้านล้านดอลลาร์ทุกวัน ดังนั้นคำตอบสำหรับคำถามเกี่ยวกับความสำคัญของพวกมันขึ้นอยู่กับบริบท: สำหรับโปรแกรมเมอร์ที่เขียนการจำลอง เมอร์เซนน์ ทวิสเตอร์มีความสำคัญมากกว่า; สำหรับวิศวกรที่พัฒนาระบบความปลอดภัย จำนวนแฟร์มาต์มีความสำคัญ

ทั้งสองตระกูลเป็นตัวอย่างที่ยอดเยี่ยมของวิธีที่คณิตศาสตร์บริสุทธิ์เชิงนามธรรมหลายศตวรรษต่อมาพบการประยุกต์ใช้ที่สำคัญในเทคโนโลยี สร้างโลกที่เราอาศัยอยู่

การคำนวณจำนวนเฉพาะเมอร์เซนน์ส่งผลต่อการพัฒนาทคโนโลยีอย่างไร?

การไล่ล่าหา จำนวนเฉพาะเมอร์เซนน์ ที่ใหญ่ขึ้นเรื่อย ๆ ไม่ใช่เพียงการฝึกฝนทางวิชาการเพื่อสร้างสถิติ กระบวนการนี้ทำหน้าที่เป็นตัวเร่งปฏิกิริยาสำหรับความก้าวหน้าในสาขาเทคโนโลยีหลักหลายสาขา อย่างแรก มันผลักดันให้มีการปรับปรุงอัลกอริทึมสำหรับการคูณจำนวนเต็มขนาดใหญ่อย่างรวดเร็ว เช่น อัลกอริทึมของเชินฮาเกอ-ชตราเซินหรืออัลกอริทึมของฟือเรอร์ ซึ่งพบการประยุกต์ใช้ไกลเกินทฤษฎีจำนวน — ในการประมวลผลสัญญาณ กราฟิกคอมพิวเตอร์ และวิทยาการเข้ารหัสลับ อย่างที่สอง ความจำเป็นในการตรวจสอบตัวเลขที่มีหลักหลายสิบล้านหลัก ต้องการการสร้างและการปรับให้เหมาะสมซอฟต์แวร์ประสิทธิภาพสูงสำหรับการคำนวณแบบกระจาย

โครงการ GIMPS และไคลเอนต์ Prime95 ของมันได้กลายเป็นเครื่องมือมาตรฐานสำหรับการทดสอบความเครียดของโปรเซสเซอร์และระบุข้อผิดพลาดที่หายากที่สุดในเลขคณิตทศนิยม ซึ่งส่งผลโดยตรงต่อคุณภาพของฮาร์ดแวร์ผู้บริโภค

ท้ายที่สุด โมเดลองค์กรของโครงการดังกล่าวทำหน้าที่เป็นต้นแบบสำหรับโครงการวิทยาศาสตร์พลเมืองอื่น ๆ ตั้งแต่การค้นหาสัญญาณนอกโลก (SETI@home) ไปจนถึงการพับโปรตีน (Folding@home) แสดงให้เห็นถึงพลังของปัญญา collective และทรัพยากรแบบกระจาย

เส้นขอบใหม่ในการค้นหาจำนวนเฉพาะเมอร์เซนน์คืออะไร?

เส้นขอบใหม่ที่สำคัญในการล่าครั้งนี้คือการพิสูจน์อย่างเป็นทางการของสมมติฐานเกี่ยวกับจำนวนอนันต์ของจำนวนเฉพาะเมอร์เซนน์ แม้จะมีหลักฐานเชิงประจักษ์และข้อโต้แย้งเชิงวิวัฒนาการ แต่การพิสูจน์ทางคณิตศาสตร์ที่เข้มงวดของข้อเท็จจริงนี้ยังไม่มีอยู่ การค้นพบมันจะกลายเป็นเหตุการณ์สำคัญของศตวรรษในทฤษฎีจำนวน

ในทางปฏิบัติ การค้นหายังคงเคลื่อนไปสู่สถิติใหม่ ๆ ด้วยการค้นพบใหม่แต่ละครั้ง การตรวจสอบผู้สมควรคนต่อไปต้องการทรัพยากรการคำนวณและเวลามากขึ้นเรื่อย ๆ สิ่งนี้สร้างความต้องการให้เกิดความก้าวหน้าทางอัลกอริทึมใหม่ ๆ อาจใช้การคำนวณควอนตัมหรือแนวทางใหม่โดยพื้นฐานต่อการทดสอบความเป็นจำนวนเฉพาะ นอกจากนี้ยังมีความเป็นไปได้ที่สถิติใหม่อาจถูกสร้างขึ้นด้วยความช่วยเหลือของปัญญาประดิษฐ์ ซึ่งสามารถค้นพบรูปแบบใหม่ในการกระจายตัวของจำนวนเฉพาะหรือปรับพารามิเตอร์การค้นหาให้เหมาะสม

ไม่ว่าจะมีความก้าวหน้าครั้งต่อไปอย่างไร มันจะนำเทคโนโลยีและแนวคิดใหม่ ๆ มาด้วยอย่างแน่นอน ซึ่งจะพบการประยุกต์ใช้ไกลเกินคณิตศาสตร์ ดำเนินตามประเพณีหลายศตวรรษที่เริ่มต้นโดยเมอร์เซนน์ แฟร์มาต์ และออยเลอร์ต่อไป