Разгадывая тайны Вселенной: Полное руководство по вихрю Мерсенна, числам и их влиянию на технологии

Вихрь Мерсенна (Mersenne Twister) — это очень популярный и эффективный алгоритм генерации псевдослучайных чисел (ГПСЧ), который используется в компьютерах для создания последовательностей, имитирующих случайные, например, в играх, симуляциях и статистике. Он известен своим колоссальным периодом (последовательность повторяется лишь через огромное количество чисел, ~4.3×10^6001), высокой скоростью генерации и хорошим статистическим качеством, но не подходит для криптографии, так как его состояние можно восстановить, имея 624 сгенерированных числа.

Вихрь Мерсенна — это не физическое явление, а метафорическое название, используемое в математике и компьютерных науках для описания эффективного алгоритма генерации псевдослучайных чисел, основанного на свойствах простых чисел Мерсенна. Этот алгоритм, известный как вихрь Мерсенна или Mersenne Twister, особенно ценен своей исключительно длинной периодичностью, равной числу Мерсенна M_19937, что означает 2^19937 – 1, и высоким качеством распределения случайных чисел.

Практическая ценность вихря Мерсенна заключается в его повсеместном применении для моделирования, криптографии (с оговорками), компьютерных игр и научных вычислений, где требуется надежный источник случайности. Понимание этого алгоритма неразрывно связано с изучением самих чисел Мерсенна — чисел вида M_n = 2^n – 1, которые являются простыми только при определенных условиях и которые веками будоражили умы математиков.

Именно поиск простых чисел Мерсенна, крупнейших известных простых чисел, и потребность в качественных генераторах случайных чисел для вычислительных систем привели к созданию этого выдающегося алгоритма, ставшего стандартом во многих языках программирования и системах.

Что такое вихрь Мерсенна и почему он так важен?

Когда говорят о вихре Мерсенна, чаще всего имеют в виду конкретный алгоритм — Mersenne Twister (MT19937), разработанный в 1997 году японскими учеными Макото Мацумото и Такудзи Нисимурой. Основная задача этого алгоритма — генерировать последовательность чисел, которая максимально похожа на случайную, но при этом является полностью детерминированной и воспроизводимой при задании одинакового начального значения (seed).

Это свойство критически важно для научных экспериментов, где результаты симуляции должны быть верифицируемыми. В отличие от простых линейных конгруэнтных генераторов, которые имеют короткие периоды и могут давать предсказуемые результаты, вихрь Мерсенна обеспечивает равномерное распределение чисел вплоть до 623 измерений, что делает его одним из самых надежных генераторов для общего применения.

Его разработка стала ответом на растущие потребности вычислительной математики в середине 90-х годов, когда существовавшие алгоритмы уже не справлялись с задачами моделирования сложных систем.

Каковы ключевые свойства алгоритма Mersenne Twister?

Алгоритм вихря Мерсенна обладает набором характеристик, которые делают его выдающимся инструментом. Во-первых, его период невероятно велик и составляет 2^19937 – 1, что превышает количество элементарных частиц во Вселенной. Это число является простым числом Мерсенна, отсюда и название алгоритма. Во-вторых, он обеспечивает равномерное распределение значений во всем своем пространстве состояний, что подтверждается строгими статистическими тестами, такими как Diehard tests. В-третьих, он эффективно реализуется на современном компьютерном оборудовании с использованием битовых операций и обладает хорошей производительностью. Однако важно отметить, что алгоритм не является криптографически стойким: зная достаточное количество последовательных выходных значений, можно восстановить внутреннее состояние и предсказать всю последующую последовательность. Поэтому для задач, связанных с безопасностью, используются другие специализированные генераторы.

Как используется вихрь Мерсенна в реальных приложениях?

Благодаря своим свойствам, Mersenne Twister стал стандартным генератором случайных чисел во многих популярных системах. Например, он является генератором по умолчанию в языках программирования Python (модуль random), R, Ruby, PHP и распространенных математических пакетах, таких как MATLAB. В компьютерных играх он часто используется для генерации уровней, событий и поведения неигровых персонажей, создавая разнообразный и при этом воспроизводимый игровой опыт. В научных исследованиях, особенно в методах Монте-Карло для физики, финансового моделирования и биоинформатики, этот алгоритм обеспечивает необходимую случайность для получения статистически значимых результатов.

Из личного опыта работы над проектами машинного обучения могу сказать, что инициализация весов нейронных сетей часто зависит от качественного генератора случайных чисел, и вихрь Мерсенна долгое время был надежным выбором для этой задачи, пока не появились более специализированные методы.

Как правильно инициализировать и использовать вихрь Мерсенна в трейдинге и инвестировании?

Инициализация и использование вихря Мерсенна в финансовом моделировании, алгоритмическом трейдинге и оценке инвестиционных рисков требуют особого внимания к детерминизму и качеству случайности.

Ключевой принцип — гарантированная воспроизводимость результатов бэктестинга торговых стратегий. Для этого начальное значение (seed) генератора должно быть явно зафиксировано в коде константой, а не зависеть от текущего времени системы. Это позволяет точно воссоздать всю последовательность «случайных» событий — ценовых шоков, времени исполнения ордеров — и убедиться, что прибыльность стратегии стабильна при многократных прогонах теста, а не является следствием единичной удачной симуляции.

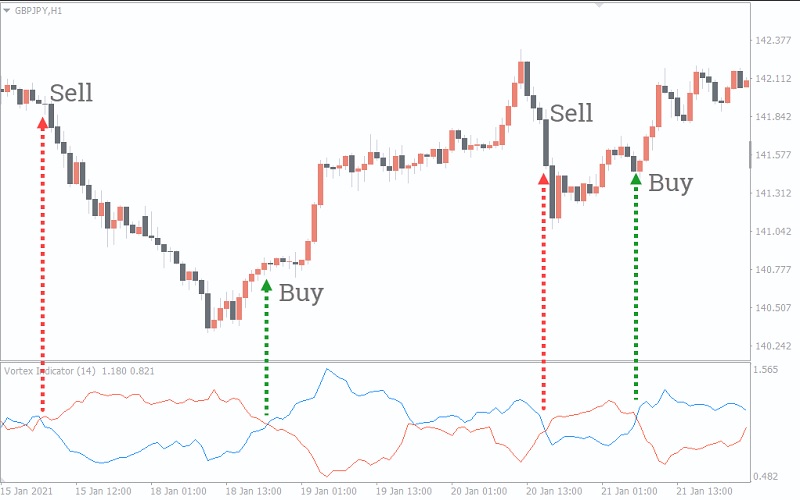
В высоконагруженных торговых системах, обрабатывающих множество потоков данных, каждый логический модуль (например, симулятор рыночных воздействий, генератор параметров для оптимизации и модуль оценки рисков) должен использовать свой собственный, изолированный экземпляр генератора с уникальным, но также детерминированным seed. Это предотвращает неявную корреляцию между случайными процессами, которая может исказить итоговую статистику, такую как максимальная просадка или Sharpe ratio.

Для моделирования путей движения цены активов, например, по методологии Монте-Карло для оценки стоимости опционов или Value at Risk (VaR), стандартного вызова равномерного распределения `random()` часто недостаточно. Необходимо преобразовать равномерно распределенную последовательность от вихря Мерсенна в другие статистические распределения, такие как нормальное или логнормальное, используя алгоритмы вроде преобразования Бокса-Мюллера. При этом критически важно осознавать и компенсировать главный недостаток алгоритма для финансовой сферы — его предсказуемость при наблюдении достаточно длинной выходной последовательности.

Хотя для чисто исследовательских целей бэктестинга это не проблема, для работы живых торговых систем, где случайность может использоваться для рандомизации времени отправки ордеров, этот фактор представляет теоретическую уязвимость. Поэтому в продакшн-среде, особенно в высокочастотной торговле, часто применяют гибридные подходы, где вихрь Мерсенна, инициализированный безопасным криптографическим seed, комбинируется с источником настоящей энтропии от аппаратных генераторов случайных чисел для периодического обновления состояния.

Практический пример из опыта риск-менеджмента: при расчете VaR для портфеля с помощью исторического моделирования методом Монте-Карло мы генерировали сотни тысяч сценариев будущих цен. Использование вихря Мерсенна с фиксированным seed на этапе разработки модели позволяло всей команде аналитиков работать с идентичными данными и согласованно проверять влияние новых факторов. Однако в финальной отчетности для регулятора seed менялся, и весь расчет повторялся тысячу раз, чтобы получить доверительный интервал для самого показателя VaR, что демонстрировало устойчивость модели.

Такой двухэтапный подход — детерминизм для разработки и верификации плюс вариативность для финальной оценки — является хорошей практикой. Он также помогает избежать «оверфитинга» торговой стратегии под конкретную случайную последовательность: если стратегия показывает прибыль только на одном, заранее заданном seed, но «просаживается» на сотне других, это явный признак статистической незначимости и подгонки под шум.

Таким образом, вихрь Мерсенна служит в финансах надежным и эффективным инструментом для создания контролируемой стохастической среды. Его правильное применение строится на трех китах: строгом детерминизме для воспроизводимости тестов, изоляции генераторов для чистоты экспериментов и осознанном переходе к вариативности и криптографически стойким источникам случайности на этапе финального анализа и в рабочих системах. Этот алгоритм позволяет трансформировать неопределенность рынка в количественно измеримые риски и возможности, обеспечивая математическую строгость в принятии инвестиционных решений.

Зачем нужны числа Мерсенна и что делает их особенными?

Числа Мерсенна, названные в честь французского монаха XVII века Марена Мерсенна, имеют вид M_n = 2^n – 1. Их изучение ведется не из абстрактного любопытства, а из-за фундаментальных связей с теорией чисел и практических приложений.

Простые числа Мерсенна напрямую связаны с совершенными числами — числами, равными сумме своих собственных делителей. Согласно теореме, доказанной еще Евклидом и позднее дополненной Эйлером, каждое четное совершенное число может быть представлено как 2^(p-1) * (2^p – 1), где (2^p – 1) — простое число Мерсенна.

Эта глубокая связь делает их ключом к пониманию структуры совершенных чисел. Кроме того, простые числа Мерсенна служат тестовыми полигонами для новых алгоритмов проверки простоты и мощных вычислительных систем, как в проекте GIMPS (Great Internet Mersenne Prime Search). Благодаря своей двоичной природе (сплошная последовательность единиц в двоичной системе) они также имеют значение в информатике, например, в построении кодов с исправлением ошибок.

Какая история стоит за поиском простых чисел Мерсенна?

Охота за простыми числами Мерсенна — это многовековая сага, полная ошибок, триумфов и технологического прогресса. Сам Мерсенн в 1644 году высказал утверждение о том, какие значения n до 257 дают простые числа, и многие из его догадок оказались неверны. Лишь с развитием математического аппарата и появлением компьютеров поиск ускорился.

Знаковым событием стало открытие в 1996 года числа M_1398269 силами проекта GIMPS, который использует распределенные вычисления тысяч добровольцев по всему миру. Каждое новое открытие самого большого известного простого числа почти всегда является числом Мерсенна, что говорит об эффективности специализированных алгоритмов проверки, таких как тест Люка-Лемера. Этот тест, разработанный в 1930-х годах, позволяет относительно быстро (по меркам теории чисел) проверить простоту числа Мерсенна, не выполняя трудоемкого деления на все возможные делители. С 1952 года все рекордные простые числа были найдены именно среди чисел Мерсенна.

Каковы практические применения чисел Мерсенна сегодня?

• Криптография: Хотя сами по себе числа Мерсенна не являются основой современных криптографических систем (как RSA), они используются для генерации больших простых чисел, необходимых в некоторых протоколах, благодаря эффективности теста Люка-Лемера.
• Тестирование компьютерного оборудования: Операции с огромными числами Мерсенна служат стресс-тестом для процессоров и систем памяти, выявляя ошибки в вычислениях с плавающей запятой и целочисленной арифметике.
• Теория кодирования: Их бинарная структура (например, M_3 = 7, что в двоичной системе 111) находит применение в построении циклических кодов и других схемах, исправляющих ошибки при передаче данных.
• Математические исследования: Они остаются центральным объектом в таких нерешенных проблемах, как гипотеза о бесконечности множества простых чисел Мерсенна, решение которой продвинуло бы вперед всю теорию чисел.

Самое значимое число Мерсенна: какое оно и почему?

На звание самого значимого числа Мерсенна претендуют несколько кандидатов в зависимости от критериев — исторической важности, математической элегантности или вычислительного триумфа. С формальной точки зрения, самым значимым на сегодняшний день является самое большое известное простое число, которое по состоянию на 2026 год также является простым числом Мерсенна. Последний рекорд, установленный в рамках проекта GIMPS, — это число M_82589933, имеющее почти 25 миллионов десятичных цифр.

Однако с исторической и концептуальной точек зрения огромную роль сыграло число M_31 = 2^31 – 1 = 2147483647. Это число является простым числом Мерсенна и долгое время было самым большим известным простым числом, найденным Леонардом Эйлером в 1772 году. Но что еще важнее, M_31 — это максимальное значение для 32-битного знакового целого числа в информатике, что сделало его фундаментальной константой в программировании, определяющей диапазоны массивов, идентификаторов и случайных чисел. Многие ранние генераторы случайных чисел, включая вихрь Мерсенна, были разработаны с учетом этого ограничения архитектуры процессоров.

Как M_31 повлиял на развитие информатики?

Число 2^31 – 1 проникло в самые основы проектирования программного обеспечения. Оно определяет максимальный положительный диапазон для типа данных `int32_t` в языках C и C++, что напрямую влияет на проектирование структур данных, индексацию массивов и генерацию уникальных идентификаторов. В эпоху 32-битных систем это число было синонимом пределов вычислительной мощности. Значение M_31 также часто служило модулем в простейших генераторах случайных чисел, так как будучи простым, оно обеспечивало хорошие статистические свойства. Это наглядный пример того, как абстрактная математическая концепция — простое число Мерсенна — становится краеугольным камнем в практической инженерии.

Из личного опыта разработки высоконагруженных систем помню, как переполнение этого предела было частым источником ошибок (так называемый Y2038 problem в Unix-времени), что подчеркивает практическую важность понимания этих математических ограничений.

Что делает проект GIMPS и как он работает?

Проект GIMPS — это ярчайший пример гражданской науки, где каждый желающий может пожертвовать вычислительные мощности своего компьютера для решения великой математической задачи. Алгоритм работы проекта построен на эффективном распределении задач:

1. Центральный сервер выдает участникам кандидатов на простоту — определенные показатели p для чисел M_p = 2^p – 1.
2. Программа-клиент (Prime95 или mprime) в фоновом режиме выполняет тест Люка-Лемера на проверку простоты этого конкретного числа Мерсенна.
3. Если кандидат проходит тест, результат перепроверяется на другом компьютере с другим программным и аппаратным обеспечением для исключения ошибок.
4. После двойной проверки открытие объявляется, и участники, обнаружившие число, могут получить часть скромного денежного приза (обычно около 3000 долларов) и, конечно, всемирную известность.

Благодаря этой децентрализованной модели, проект GIMPS за годы своей работы проверил все возможные показатели для чисел Мерсенна в огромном диапазоне, который был бы недоступен даже для суперкомпьютера. Участие в подобных проектах не только приносит пользу науке, но и является отличным способом стресс-тестирования собственного компьютерного оборудования на стабильность.

Как работает генератор случайных чисел на основе вихря Мерсенна?

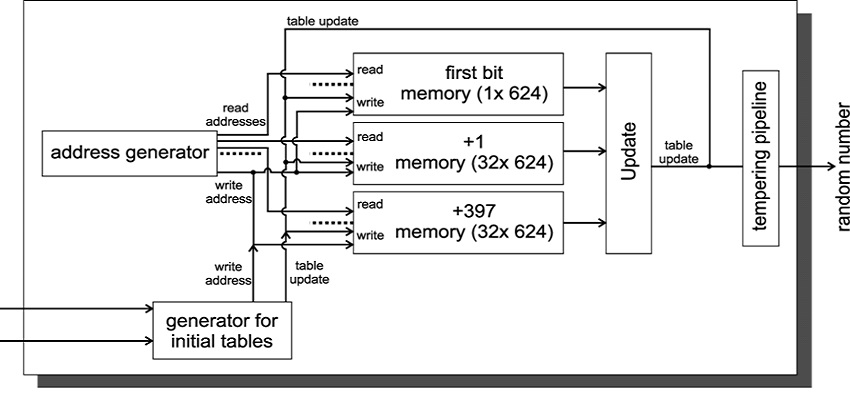
В основе работы генератора случайных чисел Mersenne Twister лежит манипуляция с внутренним состоянием — массивом из 624 тридцатидвухбитных слов. Алгоритм можно представить как циклический процесс, где на каждом шаге одно слово из этого массива подвергается серии битовых операций (сдвиги, исключающее ИЛИ, умножение) для получения выходного значения.

После того как все 624 слова использованы, состояние «перемешивается» с помощью специальной функции скремблирования (twist), что и дало название алгоритму — «вихрь». Этот процесс гарантирует, что период генератора будет равен периоду перебора всех возможных внутренних состояний, который и выбран равным простому числу Мерсенна M_19937.

Детерминизм обеспечивается тем, что при одинаковом начальном значении seed массив инициализируется одинаково, приводя к одной и той же последовательности чисел. Это критически важно для отладки программ: если симуляция ведет себя странно, разработчик может воспроизвести точно те же «случайные» события, чтобы найти ошибку.

Каковы сильные и слабые стороны этого алгоритма?

Как и любой инструмент, вихрь Мерсенна имеет свои области оптимального применения. К его неоспоримым преимуществам относятся чрезвычайно длинный период, который исключает повторение последовательности в любых практических вычислениях, и высокое качество случайности, подтвержденное множеством статистических тестов. Он также достаточно быстр для большинства задач. Однако у него есть и недостатки. Главный из них — большое внутреннее состояние (почти 2.5 КБ), что может быть проблемой для систем с ограниченной памятью, например, встроенных устройств.

Также алгоритм показывает относительно медленную инициализацию (выбор seed), что может быть заметно при необходимости частого перезапуска генератора. Но самый серьезный недостаток, о котором уже упоминалось, — это его непригодность для криптографии.

Поскольку алгоритм выдает свое внутреннее состояние в выходной последовательности, после наблюдения 624 последовательных чисел можно полностью восстановить состояние и предсказать все будущие значения. Для игр или научных симуляций это не проблема, но для шифрования данных — критический изъян.

Как правильно инициализировать и использовать вихрь Мерсенна в коде?

Правильная инициализация — залог получения качественной случайной последовательности. Простая установка seed в константу (например, 0 или 1) приведет к тому, что программа при каждом запуске будет выдавать один и тот же результат, что хорошо для воспроизводимости, но плохо для, скажем, онлайн-игры. Часто используется seed, основанный на текущем времени системы, но это тоже неидеально, если программу запускают несколько раз за одну секунду. В современных реализациях рекомендуется использовать более сложные схемы, например, сбор энтропии из различных источников ОС.

В Python, чтобы получить целое число в заданном диапазоне, следует использовать метод `randint(a, b)`, а не деление по модулю результата `random()`, так как последний может внести смещение в распределение. Для выбора случайного элемента из последовательности безопаснее использовать `random.choice(seq)`. В высоконагруженных многопоточных приложениях необходимо обеспечить, чтобы у каждого потока был свой экземпляр генератора, так как общий объект будет узким местом из-за необходимости синхронизации доступа.

Чем отличаются числа Мерсенна и числа Ферма?

Числа Мерсенна (M_n = 2^n – 1) и числа Ферма (F_n = 2^(2^n) + 1) — это два знаменитых семейства в теории чисел, каждое из которых связано с величайшими математиками и своими уникальными проблемами. Они различаются не только формулой, но и историческим контекстом, свойствами и областями применения. Пьер де Ферма предположил, что все числа такого вида являются простыми, но, как и в случае с Мерсенном, его гипотеза оказалась ошибочной: Эйлер нашел делитель у F_5. На сегодняшний день известно всего пять простых чисел Ферма (F_0-F_4), и есть предположение, что других не существует.

В то время как простые числа Мерсенна генерируют четные совершенные числа, простые числа Ферма имеют глубокую связь с геометрией — именно они появляются в задаче о построении правильных многоугольников циркулем и линейкой. Теорема Гаусса-Ванцеля утверждает, что правильный n-угольник можно построить тогда и только тогда, когда n является степенью двойки, простым числом Ферма или произведением степеней двойки и различных простых чисел Ферма.

Таким образом, эти абстрактные объекты напрямую влияют на решение древнейшей геометрической проблемы.

Где применяются числа Ферма в современном мире?

В отличие от чисел Мерсенна, которые нашли широкое применение в вычислительной технике, числа Ферма имеют более узкую, но крайне важную нишу — криптографию. Конкретно, простое число Ферма F_4 = 65537 (2^16 + 1) стало невероятно популярным выбором в качестве публичной экспоненты `e` в алгоритме RSA.

Причины этого выбора практичны и элегантны: во-первых, 65537 является простым, что гарантирует обратимость по модулю φ(n); во-вторых, его двоичное представление имеет всего две единицы (10000000000000001), что позволяет очень эффективно реализовать возведение в степень с помощью быстрого алгоритма, требующего лишь 17 операций умножения вместо тысяч. Это дает значительный выигрыш в скорости шифрования и проверки цифровых подписей на устройствах с ограниченной вычислительной мощностью, таких как смарт-карты и мобильные телефоны.

Таким образом, каждый раз, когда вы совершаете безопасную онлайн-транзакцию, вы, скорее всего, невольно пользуетесь числом Ферма.

Какое из этих семейств чисел важнее для науки и технологий?

Сравнивать важность чисел Мерсенна и Ферма — все равно что сравнивать важность колеса и рычага. Каждое семейство решает свои уникальные задачи. Для развития фундаментальной математики и вычислительных наук числа Мерсенна, безусловно, оказали большее влияние. Они связаны с совершенными числами, служат полигоном для алгоритмов проверки простоты и легли в основу одного из самых популярных генераторов случайных чисел. Их поиск стал движущей силой развития распределенных вычислений.

Числа Ферма же нашли свою судьбу в более специализированных, но критически важных областях — геометрии и криптографии. Одно конкретное число Ферма (65537) защищает триллионы долларов финансовых операций ежедневно. Поэтому ответ на вопрос об их важности зависит от контекста: для программиста, пишущего симуляцию, важнее вихрь Мерсенна; для инженера, разрабатывающего систему безопасности, — число Ферма.

Оба семейства являются блестящими примерами того, как чистая, абстрактная математика столетия спустя находит жизненно важное применение в технологии, формируя мир, в котором мы живем.

Как вычисления простого числа Мерсенна влияют на развитие технологий?

Погоня за все большими простыми числами Мерсенна — это не просто академическое упражнение для установления рекордов. Этот процесс выступает катализатором прогресса в нескольких ключевых технологических областях. Во-первых, он подталкивает к совершенствованию алгоритмов быстрого умножения больших целых чисел, таких как алгоритм Шёнхаге-Штрассена или алгоритм Фюрера, которые находят применение далеко за пределами теории чисел — в обработке сигналов, компьютерной графике и криптографии. Во-вторых, необходимость проверки чисел с десятками миллионов цифр требует создания и оптимизации высокопроизводительного программного обеспечения для распределенных вычислений.

Проект GIMPS и его клиент Prime95 стали эталонными инструментами для стресс-тестирования процессоров и выявления даже самых редких ошибок в арифметике с плавающей запятой, что напрямую влияет на качество потребительского железа.

Наконец, сама организационная модель таких проектов служит прототипом для других инициатив гражданской науки, от поиска внеземных сигналов (SETI@home) до моделирования белков (Folding@home), демонстрируя мощь коллективного интеллекта и распределенных ресурсов.

Какой следующий рубеж в поиске простых чисел Мерсенна?

Следующий большой рубеж в этой охоте — формальное доказательство гипотезы о бесконечности количества простых чисел Мерсенна. Несмотря на эмпирические свидетельства и эвристические аргументы, строгого математического доказательства этого факта до сих пор не существует. Его открытие стало бы событием века в теории чисел.

С практической стороны, поиск продолжает двигаться к новым рекордам. С каждым новым открытием проверка следующего кандидата требует все больше вычислительных ресурсов и времени. Это создает потребность в новых алгоритмических прорывах, возможно, с использованием квантовых вычислений или принципиально новых подходов к тесту простоты. Также есть вероятность, что следующий рекорд может быть установлен с помощью искусственного интеллекта, который сможет обнаружить новые закономерности в распределении простых чисел или оптимизировать параметры поиска.

Независимо от того, как будет достигнут следующий прорыв, он, несомненно, принесет с собой новые технологии и идеи, которые найдут применение далеко за пределами математики, продолжая многовековую традицию, начатую Мерсенном, Ферма и Эйлером.